Termodinamiğin Birinci Yasası

Sistem ve termal enerji kaynağı ve mekanik enerji kaynağı arasındaki ilişki 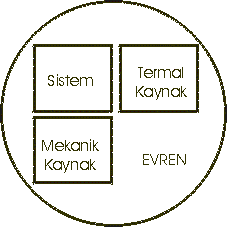Şekilde gösterilmiştir. Fiziksel kimya evreni iki kısma ayırır. Bu sistem ve çevresidir. Sistem; ilgilendiğimiz kısmıdır. Örneğin sistem, reaksiyon kabı, bir motor, elektrokimyasal bir pil, biyolojik bir hücre ve benzer şekilde örneklerin sayısı arttırılabilir. Çevre ise; bizim ölçümlerimiz gerçekleştirdiğimiz yerdir. Sistemin tipi çevre ile arasındaki sınıra bağlı olarak tanımlanabilir. Aşağıdaki şekillerde çevre ile sistem arasındaki ilişkiler gösterilmiştir. Eğer sistem ile çevre arasında madde ve enerji alışverişi varsa sistem açık sistem olarak adlandırılır. Sistem ile çevre arasında madde alışverişi yok fakat enerji alışverişi varsa sistem kapalı sistem olarak adlandırılır. Sistem ile çevre arasında madde ve enerji alışverişi yoksa sistem izole sistem olarak adlandırılır. Sistem ve çevrenin tümü ise Evreni meydana getirir.

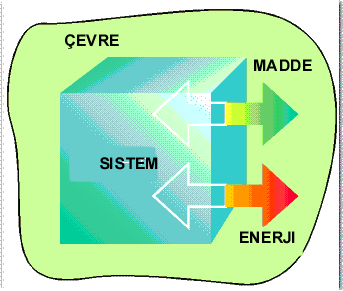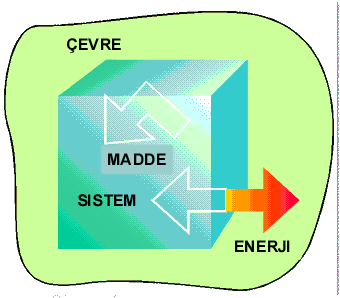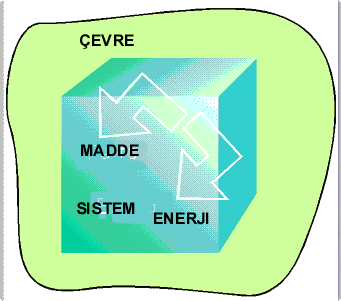Açık Sistem	Kapalı Sistem	İzole Sistem

Eğer sistemle çevre denge halinde bulunuyorlarsa bir başka deyişle; sistemin özellikleri zamana bağlı olarak değişim göstermiyorsa bu durum Termodinamik Denge Hali olarak adlandırılır. Termodinamik denge hali dinamik bir denge halidir. Çünkü belki sistemin özellikleri zamana bağlı olarak değişmez fakat sistemi meydana getiren moleküllerin özellikleri zaman içerisinde değişim gösterir.

Sistemin sahip olduğu toplam enerji İç Enerji olarak adlandırılır. Sistemin iç enerjisi, sistemi oluşturan moleküllerin kinetik ve potansiyel enerjilerinden meydana gelir. Sistem, U_i iç enerjisine sahip bir i halinden, yeni bir U_s iç enerjisine sahip s haline ulaşmışsa, sistemin iç enerji değişimi için;
DU=U_s - U_i
yazılabilir. İç enerjinin değeri yalnızca sistemin bulunduğu duruma bağlı olduğundan, iç enerji bir hal fonksiyonudur. Hal değişkenlerinden herhangi birinin değişmesi (basınç gibi) iç enerjinin değişmesiyle sonuçlanabilir. İç enerji Ekstensif bir özelliktir.

Bir sistemin iç enerjisinin değişimi, sistem üzerine iş yaparak veya sistemi ısıtarak deneysel olarak belirlenebilir. Eğer bir sistem çevresinden izole edilmişse, iç enerji değişimi meydana gelmeyecektir. Sistem üzerine bir iş yapılırsa veya sisteme bir şekilde enerji transfer edilirse sistemin iç enerjisi artacaktır. Bunu
DU = q + W
şeklinde gösterebiliriz. Bu eşitlik Termodinamiğin Birinci Yasasının matematiksel ifadesidir. Bu eşitlik bize izole bir sistemde iç enerjinin sabit olacağını gösterir. Kapalı bir sistemde iç enerji değişimi, sisteme transfer olan ısı ya da iş büyüklüğü toplamına eşittir. Eğer sisteme iş ya da ısı olarak enerji transfer ediliyorsa W > 0 veya q > 0, sistem iş yapıyor veya ısı kaybediyorsa W < 0 veya q < 0 dır.(Örnek 1 )

Şimdi enerjinin ne olduğunu bilmediğimizi düşünelim. İşin ne olduğunu bildiğimizi düşünelim. Çünkü çevrekidi bir ağırlığın azalması veya yükselmesi gözleyebiliriz. Özel bir bileşimdeki adyabatik bir sistemin sıcaklığını çeşitli yollardan ilerleyerek aynı değere getirelim. Sonuçta Sistem üzerine 1 kJ mekanik iş yapıldığında veya 1 kJ lük elektriksel iş yapıldığında aynı sıcaklığa ulaşılır. Termodinamiğin birinci yasasının temel ifadesi bu tip pekçok gözlem sonucunda;

Adyabatik bir sistemin özel bir halden başka bir özel hale ulaşması için gereken iş miktarı aynıdır.
diye özetlenir.

Adyabatik bir sistemin bir i halinden, bir s son haline ulaşırken W_ad işinin yapıldığını düşünelim. Bu İşin herhangi bir türü (mekanik veya elektriksel) kullanılarak ve farklı ara durumlardan (örneğin farklı sıcaklık ve basınçlardan ) geçerek f haline ulaştığını düşünelim. Eğer termodinamiğin birinci yasasını bilmiyorsak, iş için W_ad(mekanik) veya W_ad(elektriksel) yazma ihtiyacını hissedebiliriz. Bununla beraber termodinamiğin birinci kanunu, işin tüm yollardan bağımsız olduğunu ve yalnızca başlangıç ve son hallere bağlı olduğunu söyler.

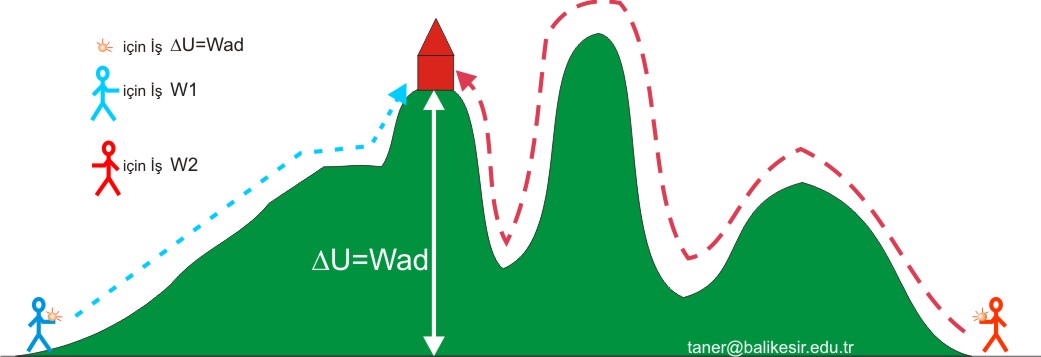
Bu sonuç dağa tırmanma olayı ile parelelelik gösterir. dağdaki bir noktaya ulaşmak için hangi yolu kullanırsak kullanalım. yaptığımız iş, iki nokta arasındaki yükselti farkına bağlıdır. Bu fark aslında iki durum arasındaki iç enerji farkı kadardır.
W_ad = U_s - U_i = DU
Bu eşitlik, adyabatik bir sistemdeki iş miktarının hesaplanması için iki durum arasındaki iç enerji farkını bulmamız gerektiğini söyler.

Şimdi aynı olayın kapalı bir sistemde gerçekleştiğini düşünelim. Bu durumda sistem çevresi ile termal temas halindeyken yine i başlangıç halinden, s haline ulaştığını düşünelim. İç enerji değişimi bir önceki hesaplamadaki kadar olacaktır. Çünkü U bir hal fonksiyonu olduğunu daha önce söylemiştik. Bununla beraber bu tür bir sistemde sistem üzerine yapılan işin bir kısmı ısı olarak sistemden uzaklaşacaktır. Uzaklaşan miktar ise;
q = W_ad - W
eşitliği ile verilebilir. Ayrıca DU = W_ad olduğundan;
q = DU - W
yazılabilir. Bununla beraber Bu eşitlik matematiksel olarak daha önce çıkartılan eşitliğe benzerdir.

E l e k t r o n i k    K a y n a k l a r

Joule's Law

Joule's Mechanical Equivalent of Heat Apparatus

Joule's Equivalent

James Prescott Joule (1818 - 1889)