Hal Fonksiyonlarının Bazı Özelllikleri
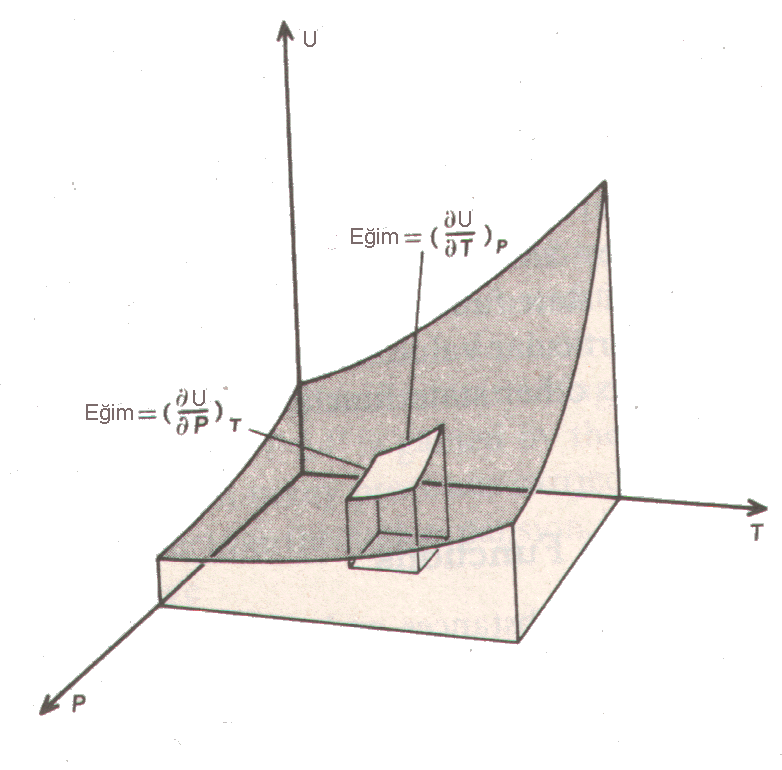
Şekil 1 : Basınç ve sıcaklığın bir fonksiyonu olarak iç enerjinin değişimi.
|
Kimyasal maddelerin ve reaksiyonların özelliklerini tanımlayabilmek için, bu özelliklerin birbirleri ile
ilişkilerini tanımlayabilmemiz gerekir.
İç enerji açısından bu bağımlılığı U=f(T,P) şeklinde gösterebiliriz.
\rm \Big( {\partial U \over \partial T}\Big)_P \; ve \; \Big( {\partial U \over \partial P}\Big)_T
olarak gösterebiliriz. İç enerji için toplam difransiyel
\rm dU = \Big( {\partial U \over \partial T}\Big)_P dT + \Big( {\partial U \over \partial P}\Big)_T dP
yazılabilir. İç enerji değişimi genellikle sıcaklık ve hacmin bir fonksiyonu olarak,
\rm dU = \Big( {\partial U \over \partial T}\Big)_V dT + \Big( {\partial U \over \partial V}\Big)_T dV
Şeklinde, entalpi ise sıcaklık ve basıncın fonksiyonu
\rm dH = \Big( {\partial H \over \partial T}\Big)_P dT + \Big( {\partial H \over \partial P}\Big)_T dP
olarak ele alınır.
Kısmi türevleri içeren eşitlikler için genelde dört yardımcı noktaya dikkat etmek gerekir.
-
\rm \Big( {\partial U \over \partial T}\Big)_V ve
\rm \Big( {\partial U \over \partial V}\Big)_T
kısmi türevleri T ve V nin fonksiyonu olduklarından
\rm \Big[ { \partial \over \partial V} \Big( { \partial U \over \partial T} \Big)_V \Big]_T = { \partial ^2 U \over \partial V \partial T} = { \partial ^2 U \over \partial T \partial V } = \Big[ { \partial \over \partial T} \Big( { \partial U \over \partial V} \Big)_T \Big]_V
yazılabilir.
-
Süreçler için fonksiyon sabit kalıyorsa, örneğin dU=0 ise;
\rm dU = \Big( { \partial U \over \partial T } \Big)_V dT + \Big( { \partial U \over \partial V } \Big)_T dV = 0
yazabiliriz. Bu eşitlik kısmi türev kurallarına göre yeniden düzenlenirse;
\rm \Big( {\partial V \over \partial T} \Big)_U = - { ( \partial U / \partial T)_V \over ( \partial U / \partial V)_T } \; veya \;
\Big( {\partial T \over \partial V} \Big)_U = - { ( \partial U / \partial V)_T \over ( \partial U / \partial T)_V }
yazılabilir.
-
Eğer bir türev toplam difransiyellerden oluşuyorsa, örneğin ;
\rm dU = \Big( {\partial U \over \partial T}\Big)_V dT + \Big( {\partial U \over \partial V}\Big)_T dV
eşitliği için dT veya dV ye bölünerek
\rm
{ \partial U \over \partial T } = \Big( { \partial U \over \partial V } \Big)_T { \partial U \over \partial T } +
\Big( { \partial U \over \partial T } \Big)_V \; veya \;
{ \partial U \over \partial V } = \Big( { \partial U \over \partial T } \Big)_V { \partial U \over \partial V } +
\Big( { \partial U \over \partial V } \Big)_T
eşitlikleri yazılabilir.
-
Aynı değişkenlerin sabit tutulduğu türevler ve kısmi türevler, kesirler halinde kullanılabilir. Örneğin
\rm {dV \over dP} için;
\rm { dV \over dP } = { dV \over dU }{ dU \over dP }
Benzer şekildeki kısmi türev işlemi için;
\rm \Big( { \partial V \over \partial P } \Big)_T =
\Big( { \partial V \over \partial U } \Big)_T \Big( { \partial U \over \partial P } \Big)_T
yazılabilir.
Bunlara benzer eşitlikler ideal gazların davranışlarını açıklamak için kullanılır.
|
