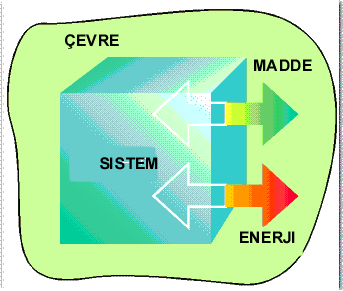
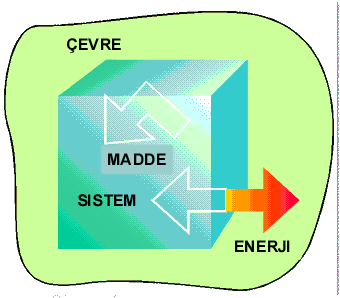
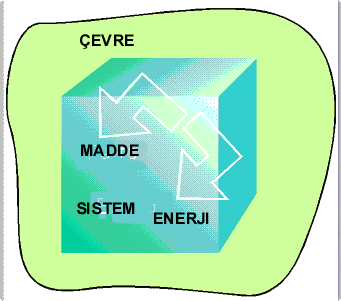
Termodinamiğin Birinci Kanunu Sistem, Çevre ve Evren Termodinamik açıdan biçim ve boyutları ne olursa olsun evrenin keyfi olarak tanımlanmış kısmı Sistem olarak adlandırır. Sistem bir molekül, bir bardak su, bir yüzme havuzu olabilir. Sistemin dışında kalan gerçek veya hayali sınırlar ile ayrılmış ölçümlerimizi gerçekleştirdiğimiz yer Çevre olarak adlandırılır. Sistem ve çevrenin tümü ise Evren olarak tanımlanır. Sistemin tipi çevre ile arasındaki sınıra bağlı olarak tanımlanır. Şekil 1 de çevre ile sistem arasındaki ilişkiler gösterilmiştir. Eğer sistem ile çevre arasında madde ve enerji alışverişi varsa sistem açık sistem olarak adlandırılır (Şekil 1 A). Sistem ile çevre arasında madde alışverişi yok fakat enerji alışverişi varsa sistem kapalı sistem olarak adlandırılır (Şekil 1 B). Sistem ile çevre arasında madde ve enerji alışverişi yoksa sistem izole sistem olarak adlandırılır (Şekil 1 C). 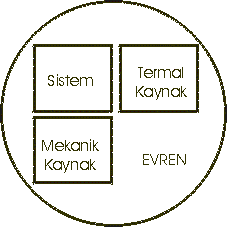(A) (B) (C) Şekil 1 : (A) Açık Sistem (B) Kapalı Sistem (C) İzole Sistem Örnek olarak sistem ve termal enerji kaynağı ve mekanik enerji kaynağı arasındaki ilişki Şekil 2 de gösterilmiştir. Şekil 2 : sistem, termal enerji kaynağı ve mekanik enerji arasındaki ilişki. Eğer sistemle çevre denge halinde bulunuyorlarsa bir başka deyişle; sistemin özellikleri zamana bağlı olarak değişim göstermiyorsa bu durum Termodinamik Denge Hali olarak adlandırılır. Termodinamik denge hali dinamik bir denge halidir. Sistemin özellikleri zamana bağlı olarak değişmez fakat sistemi meydana getiren moleküllerin özellikleri zaman içerisinde değişim gösterir. Sistemin sahip olduğu toplam enerji İç Enerji olarak adlandırılır. Sistemin iç enerjisi, sistemi oluşturan moleküllerin kinetik ve potansiyel enerjilerinden meydana gelir. Sistem, Ui iç enerjisine sahip bir i halinden, yeni bir Us iç enerjisine sahip s haline ulaşmışsa, sistemin iç enerji değişimi için; \rm \Delta U = U_s \;- \; U_i olarak verilir. Şekil 3 : Bir sistemde hacim, sıcaklık ve iç enerji değişimi. Şekil 3 de bir sistem için hacim, V, sıcaklık, T ve iç enerji değişimi, U 3 boyutlu grafik üzeride gösterilmiştir. Sistem i noktasındaki hacim, sıcaklık ve iç enerji değerlerinden, s noktasındaki hacim, sıcaklık ve iç enerji değerlerini sonsuz farklı yol ile ulaşabilir. Ancak sistem hangi yol ile i noktasından s noktasına ulaşmış olursa olsun, yine de iç enerji değişimi şekilden de kolayca görüleceği gibi aynı olacaktır. İç enerji büyüklüğü şekilde de görüldüğü gibi sistemin bulunduğu hale bağlı olduğundan iç enerji bir hal fonksiyonudur. Burada görüldüğü gibi sistemin bulunduğu hale bağlı fonksiyonlar hal fonksiyonlarıdır. Hal değişkenlerinden birinin değişmesi (basınç, sıcaklık gibi. ) iç enerjinin değişmesi ile sonuçlanabilir. İç enerji büyüklüğü ekstensif (madde miktarına bağlı) bir özeliktir. Bir sistemin iç enerjisinin değişimi, sistem üzerine iş yaparak veya sistemin sıcaklığı değiştirilerek deneysel olarak belirlenebilir. Eğer bir sistem çevresinden izole edilmişse, iç enerji değişimi meydana gelmeyecektir. Sistem üzerine bir iş yapılırsa veya sisteme bir şekilde enerji transfer edilirse sistemin iç enerjisi artacaktır. Sistemin iç enerji değişimini, sisteme trasfer edilen ısı ve işe göre \rm \Delta U = q + W \qquad \qquad\qquad (1) şeklinde gösterebiliriz. Bu eşitlik Termodinamiğin Birinci Yasasının matematiksel ifadesidir. Bu eşitlik bize izole bir sistemde iç enerjinin sabit olacağını gösterir. Kapalı bir sistemde iç enerji değişimi, sisteme transfer olan ısı ya da iş büyüklüğü toplamına eşittir. Eğer sisteme iş ya da ısı olarak enerji transfer ediliyorsa W > 0 veya q > 0, sistem iş yapıyor veya ısı kaybediyorsa W < 0 veya q < 0 dır. Soru 1 : Bir elektrik motoru mekanik iş olarak saniyede 15 kJ elektrik üretirken, çevreye 2 kJ ısı yaymaktadır. Elektrik motorundaki iç enerji değişimi ne kadardır? 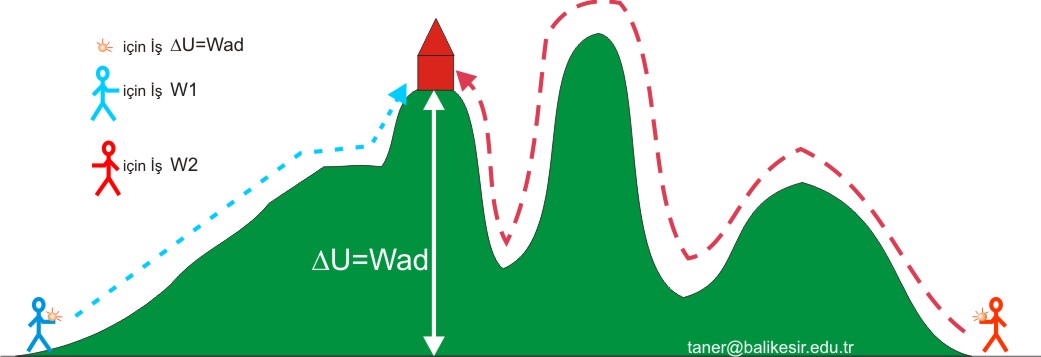Yanıt 1 : Eğer elektrik motoru saniyede 15 kJ mekanik iş ve 2 kJ çevreye ısı yayıyorsa saniyedeki iç enerji değişimi \rm \Delta U = -2 kJ - 15 kJ = -17 kJ İç enerji değişiminin negatif çıkması sistemin enerji kayıplarının bir sonucudur. Sistem 17 kJ iş yapabilme kabiliyetini yitirdi demektir. Herhangi bir ısı transferi olmasızın sistemin iç enerjideki değişim iş büyüklüğü ile ilgili olacaktır. Bu tür süreçler Adyabatik süreç olarak adlandırılır. Böyle bir süreç için q = 0 olacağından \rm \Delta U = W olarak yazılabilir. Adyabatik bir olayda sistemin bir halden başka bir özel hale ulaşması için gereken iş miktarı aynıdır. Adyabatik bir sistemin bir i halinden, bir s son haline ulaşırken Wad işinin yapıldığını düşünelim. Bu İşin herhangi bir türü (mekanik veya elektriksel) kullanılarak ve farklı ara durumlardan (örneğin farklı sıcaklık ve basınçlardan ) geçerek s haline ulaştığını düşünelim. Eğer termodinamiğin birinci yasasını bilmiyorsak, iş için Wad(mekanik) veya Wad(elektriksel) yazma ihtiyacını hissedebiliriz. Bununla beraber termodinamiğin birinci kanunu, adyabatik işin tüm yollardan bağımsız olduğunu ve yalnızca başlangıç ve son hallere bağlı olduğunu söyler. Şekil 4 : Benzer bir cismi dağın tepesindeki kulubeye taşıyan adamlar. Şekil 4 de görüldüğü gibi 2 kişinin farklı yollardan ellerindeki cismi dağın tepesindeki bir kulubeye taşıdıklarını varsayalım. Şekilden de görüldüğü gibi dolanbaçlı ve zorlu yolu seçen kişi çok enerji kaybedecektir. Çok kalori yakacaktır da diyebiliriz. Daha basit yolu seçen kişi de diğeri kadar olmasa da kalori yakacaktır. Fakat ellerindeki yük (cisim) açısından olaya bakarsanız. Hangi yoldan dağın tepesine ulaşmış olursa olsun iç enerji değişimi aynıdır. Ne dışarıdan enerji almıştır ne de enerji kaybetmiştir. Yalnızca potansiyel enerjisi değişmiştir. Bu değişim miktarı (q = 0) olduğundan yapılan adyabatik iş büyüklüğüne eşittir. Adyabatik bir sistemde i halinden s haline ulaşırken iş büyüklüğü yoldan bağımsız olarak iç enerji değişimine eşit olmasına karşın, kapalı bir sistemde gerçekleşen bir olayda sistem i halinden s haline ulaşırken sistemin iç enerji değişimi yine aynı olacaktır. Çünkü sistemin iç enerjisinin bir hal fonksiyonu olduğunu daha söylemiştik. Bununla beraber kapalı bir sistemde sistem üzerine yapılan işin bir kısmı ısı olarak sistemden uzaklaşacaktır. Uzaklaşan miktar ise; \rm \Delta q = -W_{ad} - W eşitliği ile verilebilir. Ayrıca \rm \Delta U = W olduğundan; \rm q = \Delta U - W yazılabilir. Bununla beraber Bu eşitlik matematiksel olarak daha önce çıkartılan eşitliğe benzerdir.