Matematik İle İfade Edebiliyorsanız Bilginiz Doyurucudur.
A. Huxley

En Küçük Kareler Yöntemi

En Küçük Kareler Yöntemi (Least Squares Method), iki veya daha fazla değişken arasındaki ilişkiyi modellemek için kullanılan istatistiksel bir tekniktir. Bu yöntem, tahmin edilen değerler ile gerçek ölçüm değerleri arasındaki hataları minimize etmek amacıyla geliştirilmiştir. Hatalar, gözlemler ile modelin tahmin ettiği değerler arasındaki farklar olarak tanımlanır ve bu farkların karelerinin toplamını en küçük yapan parametreler seçilir. Şekil 1 : y=f(x) fonksiyonu için çizilmiş eğri ve deneysel değerlerle uyumları arasındaki farklar. 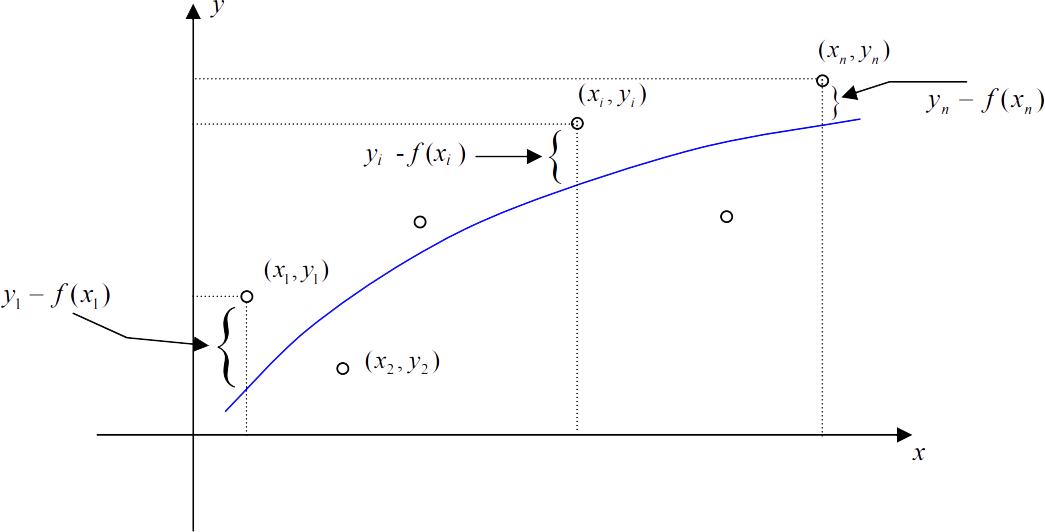Bu yöntemde bağımlı değişken y ile bağımsız değişken x arasındaki ilişki modellenmeya çalışılır. y=f(x) şeklindeki bir fonksiyona uyuyor ve herhangi bir x değeri için deneysel olarak \rm y_{ denel} değeri elde edilmişse; Bu yöntemdeki temel hedef deneysel değer \rm y_{ denel } değer ile y değeri arasındaki farkın kareleri toplamını minimize etmektir. Bu şekilde deneysel veriler ile uyuşan en iyi eğri bulunmaya çalışılır (Şekil 1). Bu toplam; \rm S=\sum _{ i=1} ^n (y_i-y_{ denel } )^2 \qquad \qquad (Eşitlik \; 1 ) şeklinde ifade edilir. Şekil 2 : y=Ax fonksiyonu için çizilmiş doğru ve fonksiyon ve deneysel veriler arasındaki uyumu sağlamak için en fonksiyonun eğimini berilrleyecek en iyi A değeri değerleri belirlenmelidir. 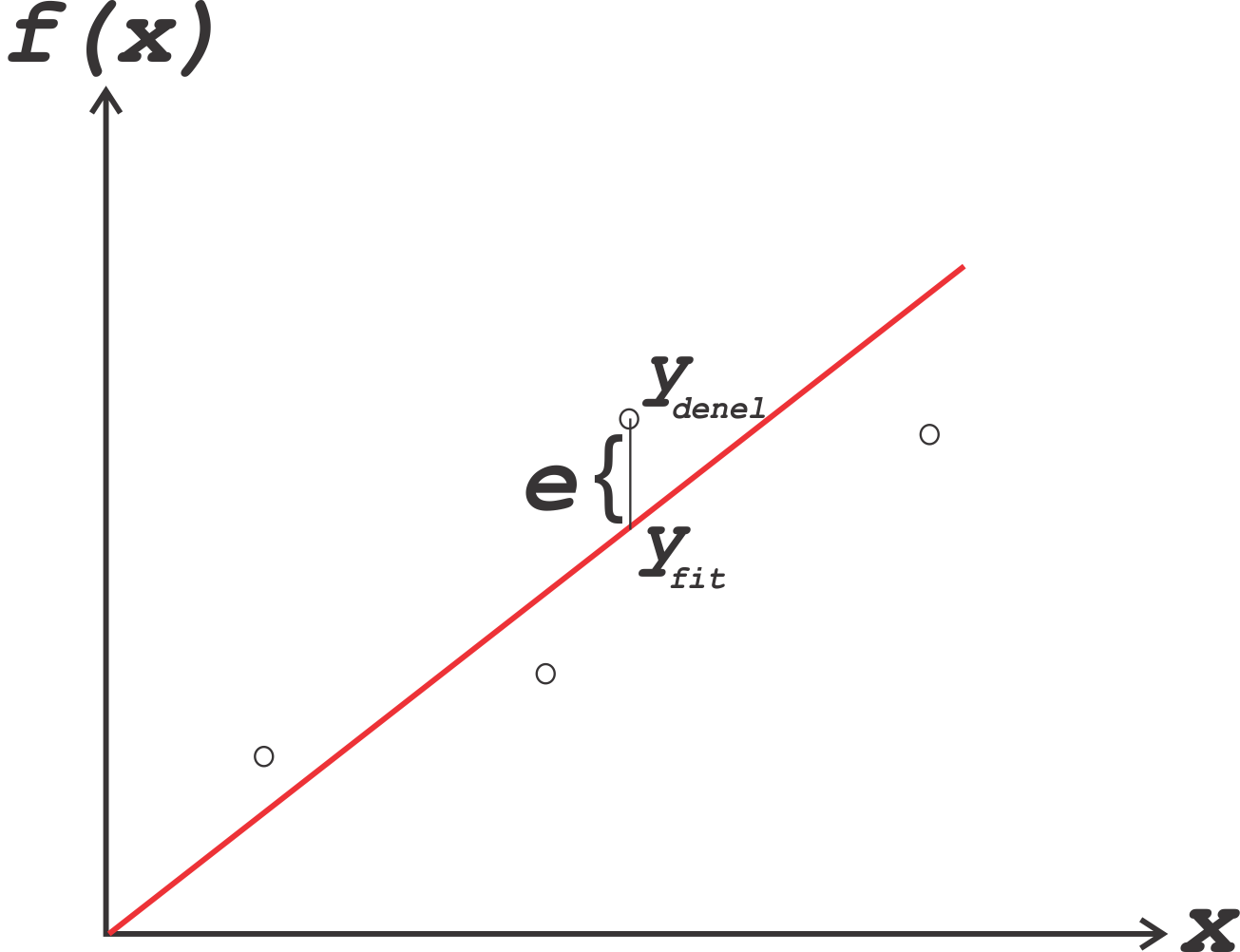y=Ax Fonksiyonu İçin Deneysel Değerlere En Yakın A Değerinin Hesaplanması f(x) = Ax fonksiyonu şeklinde bir fonksiyona uyması beklenen veriler denel yolla elde edilirken deneysel hatalar nedeni ile fonksiyonda uzaklaşacaktır. Elde edilen deneysel verilere en uygun orjinden geçen doğrunun elde edilmesi için herbir deneysel nokta ile fonksiyonun gösterdiği nokta minimize edilmelidir. Şekil 2 'de daireler deneysel olarak elde edilmiş sonuçları ( \rm y_{ denel } ), kırmızı çizgi ise bu sonuçlar için çizilmiş en iyi f(x)=Ax fonksiyonuna uyan doğruyu göstermektedir. \rm y_{ fit } ise f(x)=Ax fonksiyonuna göre \rm y_{ denel } e karşı olması gereken değeri göstermektedir. Herhangi bir i noktası için yapılan hata veya sapma \rm e = y_{ fit } - y_{ denel } kadardır. Hatalarının toplamlarının her zaman pozitif çıkması için \rm e^2 alınır. \rm e = y_{ fit } - y_{ denel } \qquad \qquad (Eşitlik \; 2 ) herhangi bir denel i noktası için; \rm e = Ax_i - y_i \qquad \qquad (Eşitlik \; 3 ) \rm e^2 = (Ax_i - y_{i(denel)})^2 \qquad \qquad (Eşitlik \; 4 ) \rm e^2 = A^2x_i^2 -2Ax_iy_{i(denel)} + y_{i(denel)}^2 \qquad \qquad (Eşitlik \; 5 ) \rm { de^2 \over dA } = 2Ax_i^2 - 2x_iy_{i(denel)} \qquad \qquad (Eşitlik \; 6 ) \rm { de^2 \over dA } = 0 yapan değer en iyi değer olacaktır. Böylece deneysel verilere uyacak en iyi A değeri; \rm A = { x_iy_{i(denel)} \over x _i ^2 } \qquad \qquad (Eşitlik \; 7 ) Tüm noktalarda yapılan sapma veya hataların toplamı ise; \rm \sum e^2 = \sum (Ax_i - y_{i(denel)})^2 \qquad \qquad (Eşitlik \; 8 ) olacağından \rm A = { \sum { x_iy_{i(denel)} } \over \sum { x _i ^2 } } \qquad \qquad (Eşitlik \; 9 ) olacaktır. Örnek Çalışma y=Ax+B Fonksiyonu İçin Deneysel Değerlere En Yakın A ve B Değerlerinin Hesaplanması y=Ax+B şeklindeki bir fonksiyon için A ve B değerlerinin hesaplanması için hataların minimize edilmesi için izlemmesi gereken adımlar aşağıda gösterilmiştir. \rm e = y_{ fit } - y_{ denel } \qquad \qquad (Eşitlik \; 10 ) herhangi bir denel i noktası için; \rm e = (Ax_i+B) - y_{i(denel)} \qquad \qquad (Eşitlik \; 11 ) \rm e^2 = (Ax_i + B - y_{i(denel)})^2 \qquad \qquad (Eşitlik \; 12 ) \rm e^2 = A^2x_i^2 + BAx_i -Ax_iy_{i(denel)} + BAx_i + B^2 - By_{i(denel)} - Ax_iy_{i(denel)} -By_i +y_{i(denel)}^2 \qquad \qquad (Eşitlik \; 13 ) \rm e^2 = A^2x_i^2 + 2BAx_i - 2Ax_iy_{i(denel)} + B^2 - 2By_{i(denel)} + y_{i(denel)}^2 \qquad \qquad (Eşitlik \; 14 ) \rm {de^2 \over dA} = 2Ax_i^2 + 2Bx_i - 2x_iy_{i(denel)}=0 \qquad \Rightarrow \qquad Ax_i^2 + Bx_i - x_iy_{i(denel)}=0 \qquad \qquad (Eşitlik \; 15 ) \rm {de^2 \over dB } = 2Ax_i + 2B - 2y_{i(denel)} = 0 \qquad \Rightarrow \qquad Ax_i + B - y_{i(denel)} = 0 \qquad \qquad (Eşitlik \; 16 ) Tüm noktalarda yapılan sapma veya hataların toplamı ise; \rm A \sum _{i=1} ^n x_i^2 + B \sum _{ i=1 } ^n x_i - \sum _{i=1} ^n x_iy_{i(denel)} =0 \qquad \qquad (Eşitlik \; 17 ) \rm A \sum _{i=1} ^n x_i + nB - \sum _{i=1} ^n y_{i(denel)} = 0 \qquad \qquad (Eşitlik \; 18 ) Eşitlik 17 (n) çarpılır ve Eşitlik 18 (-1) ile çarpılır ve taraf tarafa toplanırsa; \rm A = { n \Big( \sum _{i=1} ^n x_i y_{i(denel)} \Big ) - \Big( \sum _{i=1} ^n x_i \Big ) \Big( \sum _{i=1} ^n y_{i(denel)} \Big ) \over n \Big( \sum _{i=1} ^n x_i^2 \Big )- \Big( \sum _{i=1} ^n x_i \Big )^2 } \qquad \qquad (Eşitlik \; 19 ) elde edilir. Böylece B; \rm B={ \Big( \sum _{i=1} ^n y_{i(denel)} \Big ) -A \Big( \sum _{i=1} ^n x_i \Big )\over n} \qquad \qquad (Eşitlik \; 20 ) olarak elde edilir. Örnek Çalışma ÖDEV 1 : Bazı hesap makinaları ile regrasyon ve en küçük kareler yöntemine göre hesaplamalar yapılabilir. Hesap Makinasını kullanarak aşağıdaki veri grubu için A ve B değerlerini hesaplayınız. Elde ettiğiniz verileri Örnek Çalışma daki tabloda giriş yaparak doğru yapıp yapmadığınızı kontrol ediniz. Tablo 1 : Hesap makinasını kullanarak aşağıdaki veriler için Y=AX + B fonksiyonundaki A ve B değerlerini bulun. \rm x_i \rm y_{ denel } \rm 1 \rm 7 \rm 6 \rm 19 \rm 3 \rm 13 \rm 4 \rm 14 \rm 15 \rm 49 En küçük kareler yöntemi kullanılarak deneysel noktalar için çizilebilecek en iyi fonksiyon bulunabilir. Fakat bu çizilen fonksiyonun deneysel değerlerle ne kadar uyumlu olduğunu anlamak için istatistiksel başka hesaplamalar gerekir. İstatistiksel analizde değişkenler arasındaki ilişkileri ölçmek için korelasyon katsayısı R ve determinasyon katsayısı \rm R^2 çok sık olarak kullanılır. Korelasyon Katsayısı (R) : iki sürekli değişken arasındaki doğrusal ilişkinin gücünü ve yönünü ölçmek için kullanılır. Pearson Korelasyon Katsayısı en yaygın olandır. \rm \pm 1 arasında değer alır. Eğer değer R=+1 çıkarsa veriler arasında pozitif mükemmel bir ilişki, R=-1 çıkarsa veriler arasında negatif mükemmel bir ilişki var demektir. R=0 ise; veriler arasında ilişki yok demektir. R değerini belirlemek için aşağıdaki eşitlikten yararlanılır. \rm R={ \sum (x_i- \overline{x}) (y_i - \overline{y}) \over \sqrt{ \sum (x_i- \overline{x})^2 \sum (y_i - \overline{y})^2} } \qquad \qquad (Eşitlik \; 21 ) Örnek Hesaplama Tablo 2 : Hesap makinasını kullanarak aşağıdaki veriler için R değerini hesaplayınız. Değerleri değiştirerek yeniden hesaplamalarınız kontrol ediniz. \rm x_i \rm y_{ i } \rm x_i - \overline{x} \rm (x_i - \overline{x})^2 \rm y_i - \overline{y} \rm (y_i - \overline{y})^2 \rm (x_i - \overline{x})(y_i - \overline{y}) -2 4 -2 4 4 -1 1 -1 1 1 0 0 0 0 0 1 1 1 1 1 2 4 2 4 4 \rm \overline{ x } = 3 \rm \overline{ y } = 3 \rm \sum (x_i- \overline{x} )^2 =10 \rm \sum (y_i- \overline{y} )^2 =10 \rm \sum (x_i- \overline{x}) (y_i - \overline{y})=10 Eşitlik 21 de bilinen büyüklükler yerine konursa; \rm R={ \sum (x_i- \overline{x}) (y_i - \overline{y}) \over \sqrt{ \sum (x_i- \overline{x})^2 \sum (y_i - \overline{y})^2} } \rm R={ 10 \over \sqrt{ ( 10 ) (10)} } = 1 olarak hesaplanır. Determinasyon Katsayısı ( \rm R^2 ) : Lineer regrasyonun ne kadar verilerle uyumlu olduğunu ölçmek için kullanılır. \rm R^2 ; 0 ile 1 arasında değer alır. \rm R^2 değeri 1 ise veriler ile fonksiyon birbiri ile mükemmel uyumlu demektir. Değer sıfıra doğru yaklaştıkça veriler ile lineer bir uyumun olmadığı anlamı çıkar. \rm R^2 değerini belirlemek için aşağıdaki eşitlikten yararlanılır. Burada elde edilen değerlerin fonksiyon için kadar uyumlu olduğu araştırılır. \rm R^2= 1 - { \sum (y_i - f(x)_{fit})^2 \over \sum (y_i - \overline{y})^2 } \qquad \qquad (Eşitlik \; 22 ) Eşitlikteki \rm y_i; deneysel değerleri, \rm \overline{y} ; değerleri deneysel y değerlerinin ortalamasını, ve \rm f(x)_{fit}; x,y değerleri en küçük kareler yöntemine göre f(x)=Ax veya f(x)=Ax+B fonksiyonundaki A ve B sabit sayıları bulunduktan sonra x lerilerine karşı olması gereken y değerlerini göstermektedir. Örnek Hesaplama Öncelikle Tablo 3 de verilen değerlerin, f(x)=Ax fonksiyonu için mi yoksa f(x)=Ax+B fonksiyonu için mi geçerli olduğuna karar verilmelidir. Tablo 3 de fonksiyonun f(x)=Ax olduğu düşünülmüştür. Bu nedenle x,y verilerinin f(x)=Ax olduğu düşünülerek, bu veri seti için A değeri hesaplanmalıdır. Bu hesaplama için Eşitlik 9 kullanılarak A değeri öncelikli olarak bulunmalıdır. Ardından bulunan A değeri dikkate alınarak f(x)=Ax fonksiyonuna göre f(x) değerleri belirlenmelidir. Tablo 3 : Hesap makinasını kullanarak aşağıdaki veriler için \rm R^2 değerini hesaplayınız. Değerleri değiştirerek yeniden hesaplamalarınız kontrol ediniz. \rm x_i \rm y_{ i } (deneysel) \rm x_i y_{ i } \rm x_i ^2 \rm A \rm f(x)= 1 x \rm y_i - \overline{y} \rm (y_i - \overline{y})^2 \rm y_i - f(x)_{fit} \rm (y_i - f(x)_{fit} )^2 1 1 \rm A = { \sum x_iy_{i(denel)} \over x _i ^2 } \rm A={ 55 \over 55} = 1 f(1)=(1)(1) f(1)=1 (1-3) -2 4 (1-1) 0 0 4 4 f(2)=(1)(2) f(2)=2 (2-3) -1 1 (2-2) 0 0 9 9 f(3)=(1)(3) f(3)=3 (3-3) 0 0 (3-3) 0 0 16 16 f(4)=(1)(4) f(4)=4 (4-3) 1 1 (4-4) 0 0 25 25 f(5)=(1)(5) f(5)=5 (5-3) 2 4 (5-5) 0 0 \rm \overline{y} = 3 55 55 10 0 A değeri 1 olduğundan; buradaki x değerlerine karşı olması gereken f(x) değerlerini hesaplayıp tabloda yerine koyalım. Tablo 3 de elde edilen değerler Eşitlik 22 de yerine konursa; \rm R^2= 1 - { \sum (y_i - f(x)_{fit})^2 \over \sum (y_i - \overline{y})^2 } \rm R^2= 1 - { 0 \over 10 }=1 olarak elde edilir. Bu elde edilen bilgi bu model için doğruluk oranının % 100 olduğunu göstermektedir.