| Ana Sayfa  | Dersler | Ders Programı | Simülasyonlar  | Diğer | İletişim |

Hidrojen Benzeri Atomlar İçin Schrödinger Denklemi Hidrojen benzeri atomlar \rm H, \; He^+, \; Li^{+2}, \; Be^{+3}, \; U^{+91} gibi Z atom numaralı ve bir elektrondana meydana gelmiş atomlardır ya da iyonlardır. Bu tip bir atomda, elektron çekirdekle etkileşim Coulomb İntegrali, \rm V(r)={ -Z e^2 \over 4 \pi \epsilon _o r} \qquad \qquad (Eşitlik \; 1 ) dir. Buradaki \rm \epsilon _o ; vakum geçirgenliği r ise elektronun çekirdekten uzaklığıdır. Iki zıt yüklü parçacık arasındaki etkileşim potansiyel enerjisi negatiftir. Çünkü yükler sonsuz uzaklıkta olduklarında etkileşim sıfırdır ve daha küçük r değerleri için negatiftir. Hidrojen benzeri atomlar için Hamiltonian kütle merkezi kinetik enerji terimi ve göreli hareketin kinetik enerjisi terimini içerir. Kütle merkezinin hareketi ilgilenmeyip, atomu uzayda sabit bir nokta olarak alabiliriz. İki parçacığın göreli hareketi indirgenmiş kütle kullanılarak gösterilebilir. 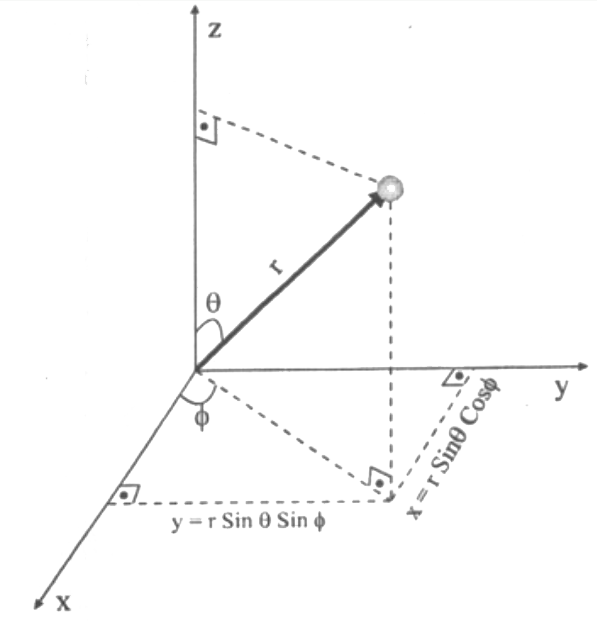Böylece Hamiltonian; \rm H=-{ \hbar ^2 \over 2 \mu } \nabla ^2 - { Z e^2 \over 4 \pi \epsilon _o r } \qquad \qquad (Eşitlik \; 2 ) olarak yazılabilir. Coulomb integrall küresel simetriye sahiptir (yani açıdan bağımsız ve yalnızca r 'ye bağlıdır.). Hamilton operatörü yazılırken polar küresel koordinatları kullanmak daha uygun olacaktır. \rm \nabla , ayrıntıları burada verilmemiştir ancak açısal momentum operatörüne bağlıdır. Yukarıdaki eşitlik \rm \nabla ^2 \Psi + {2 \mu \over \hbar ^2 } \Big(E+ { Ze^2 \over r} \Big)\Psi = 0 \qquad \qquad (Eşitlik \; 3 ) şeklinde tekrar düzenlenebilir. Küresel koordinatlara dönüştürülerek \rm { 1 \over r^2 } { \partial \over \partial r} \Big( r^2 { \partial \Psi \over \partial r} \Big) + {1 \over r^2 Sin \theta } { \partial \over \partial \theta } \Big( Sin \theta { \partial \Psi \over \partial \theta }\Big) + {1 \over r^2 Sin^2 \theta } {\partial ^2 \Psi \over \partial \phi^2 } + { 2 \mu \over \hbar } \Big( E + { Ze^2 \over r} \Big) \Psi =0 şeklinde yazılabilir. Şekil 1 : Küresel polar koordinatlarda bir parçacığın yeri. Yukarıdaki eşitlik üç farklı difransiyel eşitlik şeklinde yazılabilir. Bu nedenle hidrojen benzeri atomların dalga fonksiyonu üç ayrı fonksiyonun çarpımı olarak yazılabilir. \rm \Psi ( r, \theta , \phi) = R(r) \Theta ( \theta ) \Phi ( \phi ) \qquad \qquad (Eşitlik \; 4 ) Yukarıdaki dalga fonksiyonunu oluşturan R(r), n ve 1 kuantum sayılarına bağlıdır. \rm \Theta ise; l ve \rm m_l , kuantum sayılarının fonksiyonudur. \rm \Phi ise; \rm m_l kuantum sayısının bir fonksiyonudur. Atomik Orbitaller ve Enerjileri Hidrojene benzer atomların dalga fonksiyonları orbital olarak adlandırılır. Tüm orbitaller Eşitlik 4 formundadır. Tablo 1 : Hidrojen benzeri atomların radial dalgafonksiyonları. Orbital n l \rm R_{n, l} 1s 1 0 \rm 2 \Big( { Z \over a_o } \Big)^{3/2 } e^{- { 1\over 2} \rho } \qquad \qquad \rho= { 2Zr \over n a_o} 2s 2 0 \rm {1 \over 2 \sqrt{ 2}} \Big( { Z \over a_o } \Big)^{3/2 } (2 - \rho) e^{- { 1\over 2} \rho } \qquad \qquad \rho= { 2Zr \over n a_o} 2p 2 1 \rm {1 \over 2 \sqrt{ 6 }} \Big( { Z \over a_o } \Big)^{3/2 } \rho e^{- { 1\over 2} \rho } \qquad \qquad \rho= { 2Zr \over n a_o} 3s 3 0 \rm {1 \over 9 \sqrt{ 3 }} \Big( { Z \over a_o } \Big)^{3/2 } (6 - 6 \rho + \rho ^2) e^{- { 1\over 2} \rho } \qquad \qquad \rho= { 2Zr \over n a_o} 3p 3 1 \rm {1 \over 9 \sqrt{ 6 }} \Big( { Z \over a_o } \Big)^{3/2 } (4 - \rho ) \rho e^{- { 1\over 2} \rho } \qquad \qquad \rho= { 2Zr \over n a_o} 3d 3 2 \rm {1 \over 9 \sqrt{ 30 }} \Big( { Z \over a_o } \Big)^{3/2 } \rho ^2 e^{- { 1\over 2} \rho } \qquad \qquad \rho= { 2Zr \over n a_o} R fonksiyonu tablodaki fonksiyonlardan biridir. Herbir orbital \rm n, \; l, \; ve \; m_l kuantum sayıları ile belirlenir. Bir elektronun bu dalga fonksiyonlarından biri tarafından tanımlandığında orbitalin doldurulduğunu söyleriz. Kuantum sayılarından ikisi \rm l \; ve \; m_l açısal çözümlerin sonucudur ve çekirdek etrafındaki elektronun açısal momentumu ile ilişkilidir. Kuantum sayısı l olan bir orbitaldeki elektronun açısal momentumunun büyüklüğü \rm [l(l+1)]^{1/2} \; \hbar \qquad \qquad l=0,1,2,3,...,n-1 kadardır. Eğer \rm m_l kuantum sayılı bir orbitalde elektron varsa bu elektronun açısal momentumunun z-bileşeni; \rm m_l \; \hbar \qquad \qquad m_l = 0, \pm 1, \pm 2, \pm 3, ..., \pm l dir. n ana kuantum sayısı olarak adlandırılır ve 1, 2, 3, ... değerlerini alabilir. Enerji büyüklüğü ise; \rm E_n=- { hc \Re \over n^2} \qquad \qquad \Re = { Z^2 \mu e^4 \over 32 \pi ^2 \epsilon _o ^2 \; \hbar ^2} \qquad \qquad (Eşitlik \; 5 ) olarak ortaya çıkar. Hidrojen benzeri atomlardaki elektronun enerjisi \rm l \; ve \; m_l kuantum sayılarından bağımsız ve yalnızca ana kuantum sayısı n'e bağlıdır. Bu nedenle aynı n ile tanımlanan tüm orbitaller dejeneredirler. Radial Dağılım Fonksiyonları Şekil 2 : (a) \rm d au hacim elemanı içerisinde ölçüm yapabilen bir dedektör elektron yoğunluğunu en fazla çekirdek üzerinde belirleyecektir. (b) dedektör \rm 4 \pi ^2 d au hacminde ölçüm yapabilen bir dedektör ise elektron yoğunluğunu en fazla çekirdekten Bohr yarıçapı uzaklıkta belirleyecektir. 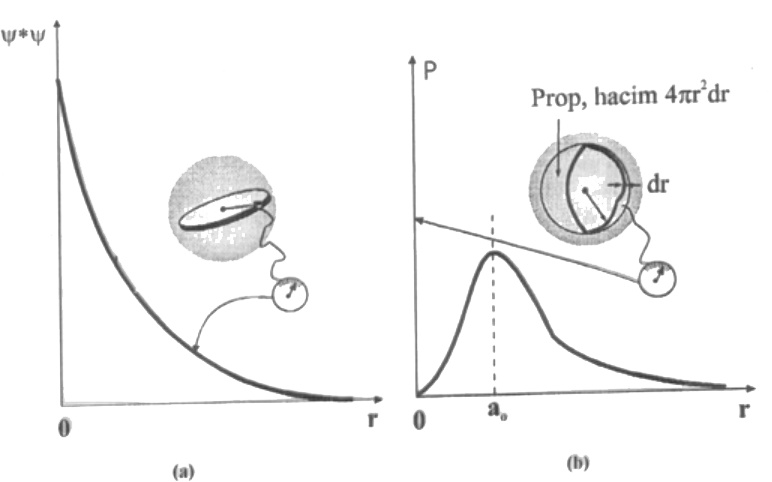Dalga fonksiyonlarını kullanırken \rm \Psi ^2 'nin herhangi bir bölgede bir elektronun bulunma ihtimali olduğunu söylemiştik. Elektronların çekirdek etraflarındaki dağılımlarını ölçebilmek için bir \rm d au hacmindeki elektron yoğunluğunu ölçebilen bir sayaç düşünelim (Şekil 2). Böylece bir hidrojen atomunun çekirdeğinden daha uzaklara doğru sayaçı hareket ettirerek bu noktalardaki ( \rm d au hacmindeki) elektron yoğunluklarını belirleyebiliriz. Hidrojen atomunun temel halindeki olasılık yoğunluğu dedektörden " \rm \Psi ^2 \quad \alpha \quad e^{-2r/a_o} \; \; \text{( dalga fonksiyonu e nin üstel fonksiyonu ile orantılıdır.)} " olarak okunur. O halde sayaç çekirdekten uzaklaştırıldığında olasılık yoğunluğu üstel olarak azalacaktır. Şimdi r yarıçapında \rm dr kalınlığında küresel bir kabuk üzerinde elektronun bulunma olasılığını hesaplamaya çalışalım. Bu kez kullanılan probun \rm 4 \pi ^2 d au olan bir kabuktaki elektron yoğunluğunu ölçtüğünü düşünelim (Şekil 2. 2b). Elektronun bu kabuk içinde bulunma olasılık yoğunluğu propun hacmi ile r yarıçapının çarpılmsı ile elde edilecektir. \rm \Psi ^2 4 \pi r^2 dr = Pdr \qquad \qquad P=\Psi ^2 4 \pi r^2 Radial dağılım fonksiyonu P, olasılık yoğunluğudur ve dr ile çarpıldığında r yarıçaplı dr kalınlığındaki kabukta elektronun bulunma ihtimaalini verir. 1s orbitali için \rm P= r^2 r^{-2r/a_o} olacaktır. Bu nedenle P, yarıçap, \rm r^2 , ile artacak fakat \rm \Psi ^2 . azalacaktır. P, çekirdek üzerinde sıfır olacaktır (r = 0). Ayrıca sonsuz uzaklıkta üstel terim sıfır olacağından P sonsuzda da sıfırdır. O halde özel bir r yarıçapında maksimum bir değer elde edilecektir ki bu değere Bohr yarıçapında ulaşılır. Soru 1 : Z atom numaralı hidrojene benzer bir atomun 1s orbitalinde elektronun bulunacağı en olasılıklı yer neresidir? Çözüm: Hidrojene benzer atomların 1s orbitallerinin dalga fonksiyonu \rm \Psi = \Big( { Z^3 \over \pi a_o^3 } \Big)^{1/2} e^{-Zr/a_o} dir. Maksimum bulunma ihtimali için dP/dr = 0 olmalıdır. Bu nedenle; \rm P=4 \pi r^2 \Psi ^2 = { 4Z^3 \over a_o ^3} r^2 e^{-2Zr/a_o} \rm {dP \over dr } = { 4 Z^3 \over a_o^3 } \Big( 2r - { 2Zr^2 \over a_o } \Big) e^{-2Zr/a_o} =0 \qquad \qquad r = r^*= {a_o \over Z} H He Li Be B C N O F Ne \rm r^* / pm 52.9 26.5 17.6 13.2 10.6 8.82 7.56 6.61 5.88 5.29