Siyah Cisim Işıması (Black Body Radiation) Bir madde yüksek sıcaklığa çıkartıldığında radyasyon yayar. Örneğin kızdırılmış bir metal çubuk kızarır. Bu olayın nedeni ısı uyarmaları sonucu cismin yüzey kısmında bulunan elektrik yüklerinin bir ivme kazanması ve elektromagnetik dalga yayması şeklinde anlatılır. Klasik kurama göre; ivmeli hareket eden elektrik yükleri elektromagnetik dalga yayar. Değişik değerde ivmelerin oluşturduğu ısı ışıması bu bölge için geçerli tüm dalga boyu şeridini içerir. Bu modele göre; birim yüzeyin yaydığı güç, cismin mutlak sıcaklığı ile orantılıdır. Bu olayı 1897 de Stefan Şekil 1 : Farklı yasalar uyarınca \rm W _\lambda = f ( \lambda) değişim eğrileri. 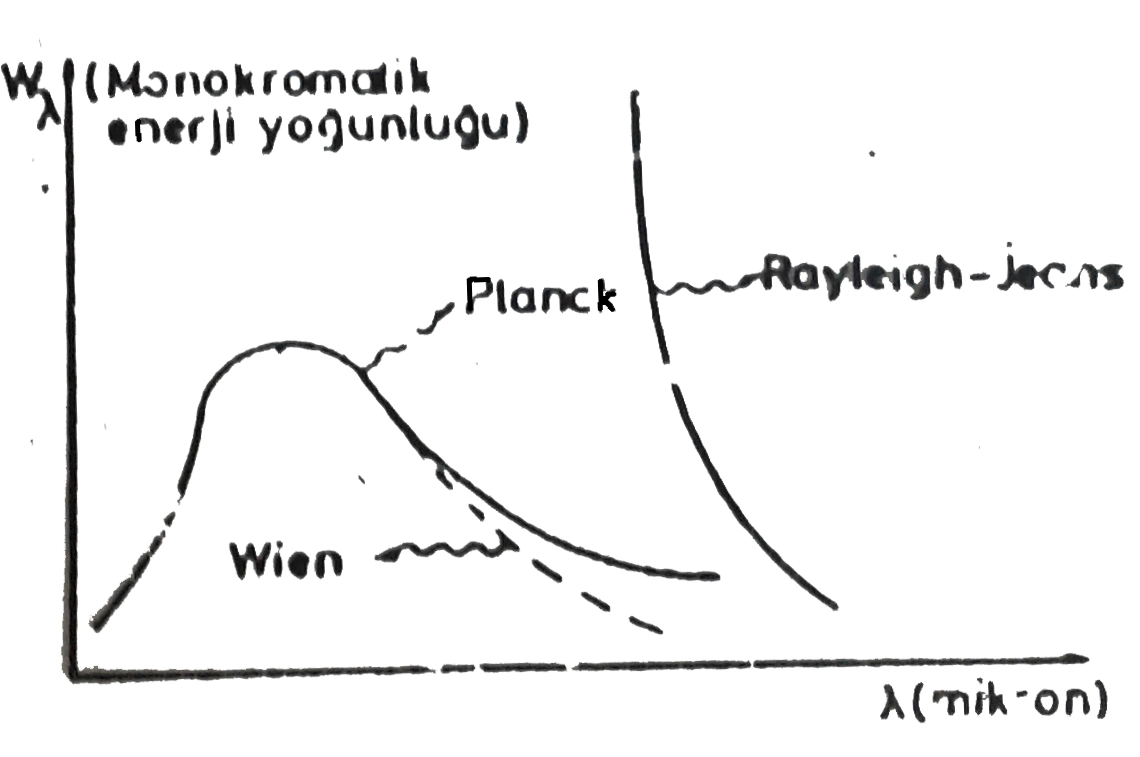\rm I(T)=e \sigma T^4 \qquad \qquad \qquad (Eşitlik \; 1) şeklindeki Eşitlik 1 ile vermiştir \rm ^*. Şekil 1 de görüldüğü gibi bir siyah cismin ışımasına ait olan eğriler ve eğrilerin maksimum değerleri dalga mekaniği tarafından doğrulanamamış ya da farklı nitelikte bulunmuştur. Bu nedenle Lummer ve arkadaşlarının şekilde de izlenen deneysel sonuçları, fizikçileri ışığın tabiatı üzerinde tamamen temel görüşleri benimsemeye zorlamıştır. Dalga teorisine göre; monokromatik ışımayla taşınan enerji, bu ışımayı oluşturan sinüzoidal dalganın genliğinin karesi ile orantılı olarak değişir. Bu düşüncenin parelelinde, polikromatik radyasyon ile taşınan enerji dalga boyu azaldığında sürekli bir artış göstermelidir. Oysa bu sonuç deneysel bulgulara ters düşmekedir. Bu nedenle siyah cisim ışıması dalga mekaniği yardımı ile açıklanamamaktadır. Nitekim Planck, ilerleyen sinüzoidal bir dalga görünümü alan monokromatik radyasyonda, enerji kuantlar halinde taşınmaktadır. hipotezi ile deneysel sonuçları açıklamada büyük katkı göstermiştir. 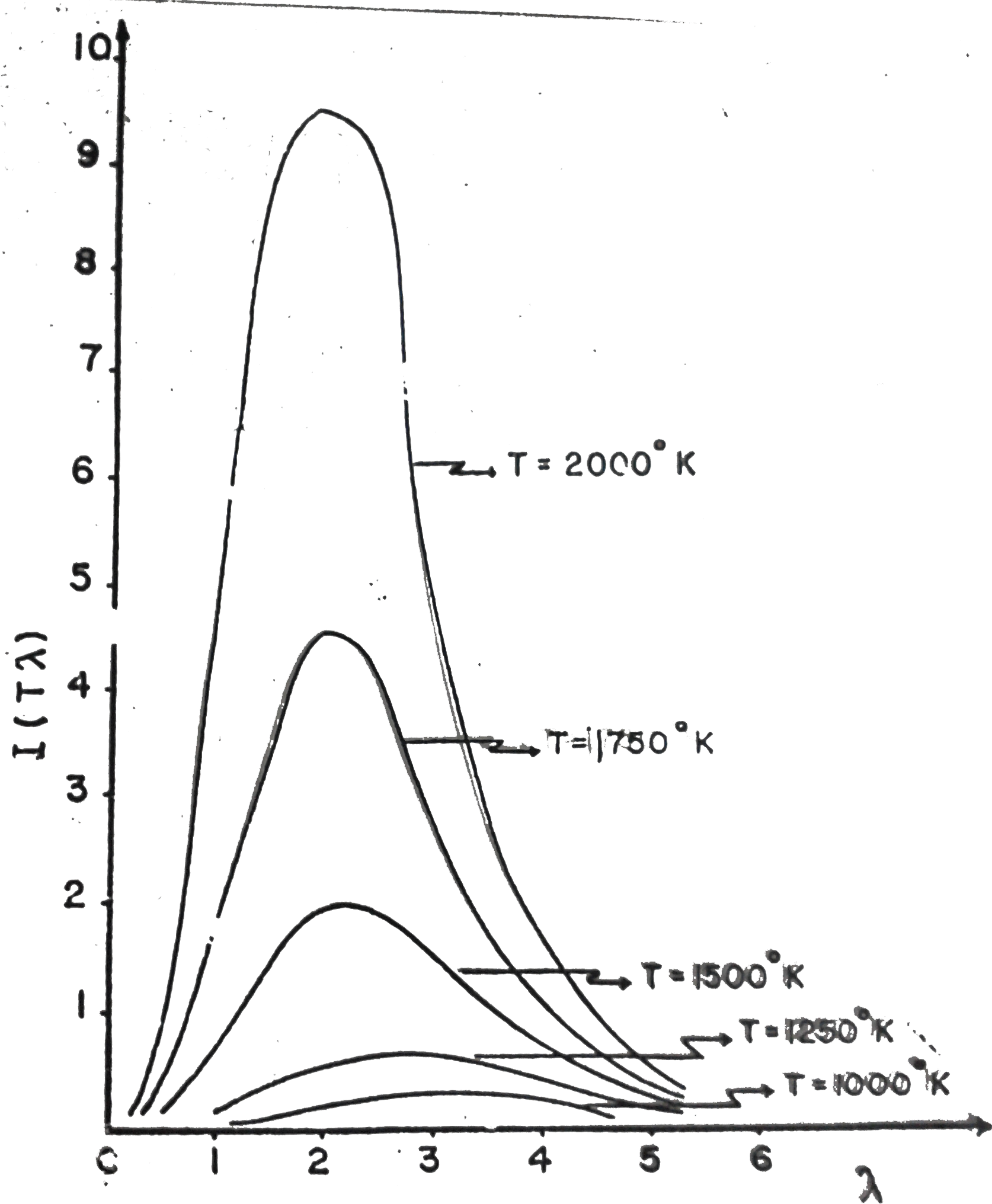Herbir kuantumun enerjisi \rm E = h \nu \qquad \qquad (Eşitlik \; 2) bağıntısı ile belirlidir ( Örnek Soru ). h; Planck sabiti, \rm \nu ; monokromatik radyasyonu frakansıdır. Deneysel sonuçların Planck Hipotezi ile açıklanması şöyle yapılabilir. Radyasyonun dalga boyu azaldığı zaman herbir kuantumun enerjiside artar. Fakat radyasyon ile taşınan kuantum sayısı azalır ve giderek sıfıra uzanır. Bir yüzeyin a; soğurganlık katsayısı yüzey tarafından soğrulan enerjinin yüzeye düşen toplam enerjiye oranı olarak belirlenir, Termodinamik düşüncelerle bu iki katsayının eşit olduğu (e = a) gösterilebilir. Bir cismin üzerine düşen bütün ışınları soğurma özelliği gösteriyorsa siyah cisim adını alır. Böyle bir cismin soğurganlık katsayısı a=1 dir. Soğurma ve yayın katsayıları eşit olduğundan siyah cisim; aynı zamanda, yüzey yüklerinde uyarım şekline dönüşen ısı enerjisinin tümünü enerji ışıması şeklinde yayan cisimdir. Diğer bir deyişle siyah cisim, üzerine düşen enerjiyi soğurduğu gibi sahip olduğu enerjiyi de yayabilen cisimdir. Eşitlik 1 de e = 1 konursa, tüm siyah cisimlerin ışıma gücünün, herhangi bir \rm cm^2 yüzey için, aynı sıcaklıkta birbirine eşit olduğu gürülür. Bunun sonucu olarak ısı ışımalarının tüm özellikleri bütün siyah cisimleri için aynıdır denilebilir. Siyah cisimmlerin ışımasına ait tayf dağılımı \rm I( \lambda T) ile belirlidir. \rm I(\lambda T), cismin \rm cm^2 lik yüzeyinden bir saniye içinde \rm \lambda ile \rm \lambda + d \lambda dalga boyu aralığında ve T sıcaklığında yayılan enerjidir. Bu şekilde elde edilmiş bir \rm I( \lambda T) \; - \; \lambda grafiği Şekil 2 'de verilmiştir. (A) (B) Şekil 2 : (A) Farklı sıcaklıklarda siyah cismin ışıma tayf dağılımı. (B) Bir metalin ısıtılması ile görünür bölgedeki renk değişimi. Görünür bölgedeki rengin kırmızıdan beyaza (tüm görünür dalga boylarına) doğru kaydığı görülmektedir. Şekil 2 den de görüldüğü gibi belli bir dalga boyu için, \rm I(\lambda T) sıcaklık yükseldikçe artar. \rm I(\lambda T) 'nin bu bölgedeki tüm dalga boyları üzerinden integrali eğri ile \rm \lambda ekseni arasında kalan alanı verir. Bu alan Eşitlik 1 bağıntısı ile tanımlanan I(T) büyüklüğüne eşittir ve sıcaklığın dördüncü kuvveti ile değişim gösterir. Her sıcaklığa ait tepe noktası T yükseldikçe küçük dalga boylarına doğru yaklaşır. Bu sonuç günlük yaşantımızdaki gözlemlerimizle uyum halindedir. Cismin sıcaklığı arttıkça yaydığı ısı çoğalır. Uzun süre ısıtılan cisimlerin önce görünen radyasyon içinde donuk kırmızı, sıcaklık arttıkça maviye kadar değişim gösteren ışınım yaydığı bilinir. Verilen bir sıcaklık içi, deneysel olarak elde edilen enerjinin dalga boyuna göre değişim eğrileri, cismin cinsine bağlı olmaksızın aynı özelliği taşır. Eğrilerin tepe noktalarına ait dalga boyları \rm \lambda _{max} \; ile \; T \; arasında; \rm \lambda _{max} T = sabit \qquad \qquad (Eşitlik \; 3) şeklinde bir bağıntı vardır. Buna Wien Yer Değiştirme Kanunu (Wien Displacement Law) denir. ( Örnek Soru 1 , ) , Wien, siyah cismin yaptığı radyasyonla ilgili enerji yoğunluğu I( \rm \lambda ) için, son şekilde gözlenen eğriyi belirleyecek biçimde aşağıdaki bağıntıyı önermiştir. \rm I( \lambda ) = c_1 \lambda ^{-5}e^{-c_2/ \lambda T} \qquad \qquad \qquad (Eşitlik \; 4) Bu bağıntı özellikle kısa dalga boyları için duyarlı değerler verir. Siyah cismin dalga boylarına göre verdiği enerji dağılımı hakkında diğer bir bağıntı Rayleigh-Jeans tarafından önerilmiştir. \rm I( \lambda ) = {8 \pi k \over \lambda ^4 } T \; = \; cT \lambda ^4 \qquad \qquad \qquad (Eşitlik \; 5) Bu bağıntı daha ziyade uzun dalga boylarında geçerli olabilmektedir. Bu eşitliğe göre \rm \lambda sıfıra yaklaştıkça \rm I( \lambda ) sonsuza yaklaşmaktadır. Bu boşluktaki enerji yoğunluğunun sonsuz olduğunu gösterir ki bu imkansızdır. Rayleigh-Jeans formülünün neden geçersiz olduğunu açıklayabilmek için, her dalga hareketinin enerjisinin belirli bir birim enerji, \rm \epsilon'un tam katları olduğunu düşünelim. Bu durumda enerji dağılımı Enerji 0 \rm 1 \epsilon \rm 2 \epsilon \rm 3 \epsilon ... Sayı \rm n_0 \rm n_1 \rm n_2 \rm n_3 ... şekilde gösterilebilir. Dağılımın Boltzmann Dağılımı ile gösterildiğini kabul edersek \rm n_i = n_oe^{- \epsilon _i \over kT} olduğunu yazabiliriz. Bu varsayımları kullanarak toplam tanecik sayısı N olmak üzere ve toplam enerjiyi hesaplayabiliriz. \rm N = \sum _i n_i = n_o + n_o e^{- \epsilon /kT } + n_o e^{-2 \epsilon /kT } + n_o e^{-3 \epsilon /kT } + ... \qquad \qquad \qquad (Eşitlik \; 6) ve \rm \chi = e^{- \epsilon/kT } olarak tanımlanırsa, yukarıdaki eşitlik \rm N=n_o(1 + \chi + \chi ^2 + \chi ^3 + ... ) \qquad \qquad \qquad (Eşitlik \; 7) şeklini alır. Parantez içindeki toplam \rm 1/(1- \chi ) 'in seriye açılmış şeklidir. Bu nedenle toplam tanecik sayısı \rm N= { n_o \over 1 - \chi } \qquad \qquad \qquad (Eşitlik \; 8) olarak gösterilebilir. Ortalama enerji \rm \overline E ' nin hesaplanması için toplam enerji aşağıdaki şekilde yazılabilir. \rm N \overline E = n_o \cdot 0 + n_1 \cdot \epsilon + n_2 \cdot 2 \epsilon + n_3 \cdot 3 \epsilon + ... \rm = \epsilon \big( n_1+ 2n_2 +3n_3+... \big) \rm = n_o \epsilon \big( \chi + 2 \chi ^2 + 3 \chi ^3 + ... \big) \rm = n_o \epsilon \chi \big( 1+ 2 \chi + 3 \chi ^2 +... \big) Ayrıca; \rm 1+2 \chi+3 \chi ^2 + ... = { d \big( 1 + \chi + \chi ^2 + \chi ^3 + . . . \big) \over d \chi } = { d \big[ 1 - \chi \big] \over d \chi } = { 1 \over \big( 1 - \chi \big) ^2 } bu matematiksel bağıntının kullanımı ile \rm N \overline E = { n_o \epsilon \chi \over \big( 1 - \chi ^2 \big) ^2 } \qquad \qquad \qquad (Eşitlik \; 9) şeklini alır. N ve \rm \chi 'in karşılıkları yerine konursa ortalama enerji \rm \overline E = { \epsilon e ^{ - \epsilon /kT } \over 1 - e ^{ - \epsilon /kT } } = { \epsilon \over e ^{ \epsilon /kT } - 1 } \qquad \qquad \qquad (Eşitlik \; 10) olarak bulunur. Ortalama enerji ile dalga boyları \rm \lambda ile \rm \lambda \pm d \lambda arasında olan hareketlerin bileşen sayısının çarpımı, dağılım fonksiyonu verir. \rm I( \lambda) = { 8 \pi \over \lambda ^4 } \Big( { \epsilon \over e^{ \epsilon /kT} - 1 } \Big) \qquad \qquad \qquad (Eşitlik \; 11) Planck \rm \epsilon ' un dalga boyu ile ters orantılı olduğunu kabul etmiştir. Frekans \rm \nu=c/ \lambda oiduğundan \rm \epsilon frekans ile doğru orantılıdır ve \rm \epsilon = h \nu = { hc \over \lambda } \qquad \qquad \qquad (Eşitlik \; 12) eşitliği ile gösterilir. \rm I( \lambda) = { 8 \pi hc \over \lambda ^5 } \Big( { \epsilon \over e^{ hc /k \lambda T} - 1 } \Big) \qquad \qquad \qquad (Eşitlik \; 13) olduğu bulunur ( Örnek Soru 1 , ). Dağılım fonksiyonu \rm I( \lambda)' yı maksimum yapan daiga boyu \rm \lambda _{max} ise; bu eşitliğin \rm \lambda' ya göre türevinin sıfıra eşitlenmesi ile bulunur. Bu şekilde; \rm \lambda _{max} T = { hc \over 4.965k } \qquad \qquad \qquad (Eşitlik \; 14) olduğu yazılabilir. ( Örnek Soru ) \rm \epsilon değeri değişik grupların enerjileri arasındaki farktır. Klasik prensiplere göre; sürekli bir enerji dağılımının olabilmesi için bu enerji farkının sıfır olması gerekir. Halbuki Planck'ın \rm \epsilon =h \nu varsayımı, enerji farkını sonlu yapmıştır. Ancaksonsuz uzunluktaki dalga boyları için fark sıfır olmaktadır. Siyah cisimde boşluğa yayılan radyasyon \rm h \nu'nün tam katları kadar enerji verebilir. Bu nedenle yayılan enerji sürekli bir dağılıma sahiptir. Enerji kuant adı verilen parçacıklar halinde yayılır. \rm ^* Burada I(T) bir saniye içinde bir \rm cm^2 lik yüzeyden bütün frekanslarda yapılan enerji ışımasını gösterir. e, yayın katsayısı olup sıfır ile bir arasında cisim özelliğine bağ olarak değer alır. \rm \sigma, ise Stefan-Boltzmann Sabiti olup değeri \rm 0.567 \times 10 ^{-4} erg \; cm^2 derece^{-1} s^{-1} dir.