| Ana Sayfa  | Dersler | Ders Programı | Simülasyonlar  | Diğer | İletişim |

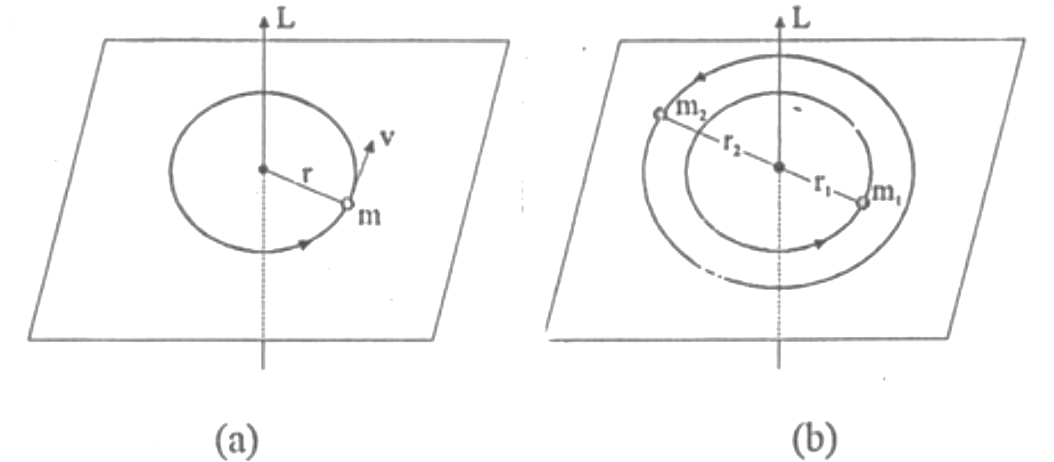
Dönme Hareketi Şekil 1 'de görüldüğü gibi, m kütleli bir parçacık r yarıçaplı dairesel bir yol boyunca xy düzlemi üzerinde hareket ediyorsa, ve bu parçağın hareket ettiği alandaki potansiyel enerjisi sıfır (V =0 ) ise; toplam enerjisi yalnızca kinetik enerjiden oluşacaktır. Bu belli yörünge içinde dönen parçacık açısal momentuma ve dönme kinetik enerjisine sahiptir. Dönen parçacığın kinetik enerjisi \rm E_k= { p^2 \over 2m } \qquad \qquad (Eşitlik \; 1 ) veya \rm E_k={ 1 \over 2} m \upsilon ^2 \qquad \qquad (Eşitlik \; 2 ) ile verilir. Fakat daha çok açısal hıza bağlı olarak ifade edilir. Parçacık \rm \nu frekansı ile r yarıçaplı bir nokta etrafında dönüyorsa parçacığın hızı \rm \upsilon=2 \pi r \nu \qquad \qquad (Eşitlik \; 3 ) ile verilebilir. Şekil 1 : (a) Sabit bir nokta etrafındaki bir kütlenin dönmesi (b) bir kütle nerkezi etrafında bir diatomik molekülün dönmesi. Buradaki açısal hız \rm \omega = (d \phi / dt) olup \rm 2 \pi \nu 'ye eşittir. Frekansın birimi \rm s^{-1} veya Hz dir. Açısal hız ise saniyede radian olarak verilir. Sabit bir nokta etrafında dönme hareketi yapan bir parçacığın kinetik enerjisi \rm E_k = {1 \over 2} m \upsilon ^2 = {1 \over 2 } I \omega^2 \qquad \qquad (Eşitlik \; 4 ) dir. I; atalet (eylemsizlik) momenti olup, bir eksen etrafında klasik bir parçacığın dönmesi için \rm I = mr^2 \qquad \qquad (Eşitlik \; 5 ) dir. Dönme kinetik enerjisi için eylemsizlik momenti lineer hareketin kinetik enerjisi için rol oynarken, açısal hız \rm \omega , lineer hız için rol oynar. Bu varsayımlara göre sağ el kuralına göre xy düzleminde dönüş yönüne göre z yönündeki açısal momentum \rm J_z ; \rm J_z = \pm I \omega = \pm m \upsilon r = \pm pr \qquad \qquad (Eşitlik \; 6 ) dir. Böylece dönme hareketinin kinetik enerjisi açısal momentuma bağlı olarak \rm E_k = {1 \over 2 } I \omega ^2 = { J_z^2 \over 2I} \qquad \qquad (Eşitlik \; 7 ) dir. Şekil 2 b deki gibi rigid bir diatomik molekül sistemi için ise; iki kütle kütle merkezleri etraflarında dönerler. Kütle merkezinin yeri \rm r_1m_1 = r_2 m_2 \qquad \qquad (Eşitlik \; 8 ) eşitliğinden bulunabilir. Çekirdekler arasındaki mesafe \rm R=r_1+r_2 olmak üzere \rm r_1 = { m_2 \over m_1 + m_2} R \; ve \; r_2 = { m_1 \over m_1 + m_2} R \; \qquad \qquad (Eşitlik \; 9 ) dir. Dönme kinetik enerjisi \rm E_k={1 \over 2 } m_1r_1^2 \omega ^2 + {1 \over 2 } m_2r_2^2 \omega ^2 \qquad \qquad (Eşitlik \; 10 ) \rm E_k={1 \over 2} \big( m_1 r_1 ^2 + m_2 r_2 ^2 \big) \omega ^2 \qquad \qquad (Eşitlik \; 11 ) \rm E_k = { 1 \over 2 } I \omega ^2 \qquad \qquad (Eşitlik \; 12 ) Burada; diatomik bir molekülün atalet momenti I; \rm I= m_1 r_1 ^2 + m_2 r_2 ^2 = { m_1 m_2 \over m_1 + m_2 }R^2 = \mu R^2 \qquad \qquad (Eşitlik \; 13 ) dir. Buradaki \rm \mu indirgenmiş kütledir. xy düzleminde dönen diatomik bir molekülün dönme kinetik enerjisi, sağ el kuralına göre z eksenindeki açısal momentuma da bağlı olarak, \rm E_k= {J_z^2 \over 2I } = { J^2 \over 2 \mu R^2 } \qquad \qquad (Eşitlik \; 14 ) olarak elde edilebilir. Kuantum mekaniğinde açısal momentumun tüm değerleri mümkün değildir. Bu nedenle hem açısal hız hemde buna bağlı olarak dönme enerjisi kuantlaşmıştır. Kuantlaşmış Dönme Enerjisi : Sağ el kuralına göre xy düzlemi üzerinde dönen sistemin dönüş yönüne bağlı olarak \rm J_z = \pm pr \qquad \qquad (Eşitlik \; 15 ) olduğundan, ayrıca de broglie bağıntısına göre \rm p = { h \over \lambda} \qquad \qquad (Eşitlik \; 16 ) olduğudan açısal momentum \rm J_z = \pm{ h r \over \lambda } \qquad \qquad (Eşitlik \; 17 ) şeklinde yazılabilir. Bu eşitlikten görüldüğü gibi r yarıçaplı yörünge üzerinde dolaşan taneciğe eşlik eden dalgaboyu kısaldıkça açısal momentum büyüyecektir. Bu son bağıntıda h sabit ve merkez etrafında dönen kütle veya bir kütle merkezi etrafında dönen sistem için r keyfi değerler alabileceğinden, açısal momentumun kesikli değerler almasının nedeni dalgaboyunun kesikli değerler almasından kaynaklanmalıdır. Şimdi dalgaboyunun neden kesikli değerler alacağını anlamaya çalışalım. Kuantum Mekaniksel Çözüm Potansiyel enerjinin sıfır olduğu xy düzleminde dönen parçacık için iki boyutlu Schrödinger Eşitliği \rm - { \hbar ^2 \over 2 m } \Big( {\partial ^2 \Psi \over \partial \chi ^2 } + {\partial ^2 \Psi \over \partial y } \Big) \qquad \qquad (Eşitlik \; 18 ) şeklindedir. Çözümü polar koordinatları kullanarak belirlemek daha iyidir. Bu nedenle; \rm \chi = r Cos \phi \qquad y=rSin \phi olup r sabit kabul edilebilir. Böylece \rm {\partial ^2 \over \partial \chi ^2 } + {\partial ^2 y \over \partial y } = { 1 \over r^2 } { d^2 \over d \phi ^2} \qquad \qquad (Eşitlik \; 19 ) yazılabilir. Böylece Schrödinger eşitliği için \rm - { \hbar ^2 \over 2mr^2} { d^2 \Psi \over d \phi ^2} =E \Psi \qquad \qquad (Eşitlik \; 20 ) yazılabilir. Atalet momenti \rm I = mr^2 olduğundan eşitlik; \rm { d ^2 \Psi \over d \phi ^2 } = { -2 IE \Psi \over \hbar ^2} \qquad \qquad (Eşitlik \; 21 ) şeklinde yazılabilir. Eşitliğin genel çözümü ise; \rm \Psi m_l = \Big( { 1 \over 2 \pi } \Big)^{1/2} e^{im_l \phi } \qquad m_l= \pm \Big( {2IE \over \hbar ^2 } \Big)^{1/2} \qquad \qquad (Eşitlik \; 22 ) dir. \rm m_l ; boyutsuz bir kuantum sayısıdır. Bu genel çözümden öyle uygun değerler seçilmelidir ki dalga fonksiyonu tek bir değere sahip olmalıdır. Bunun için dönme sınır şartı yerine getirilmelidir ve tam bir dönme sonucunda aynı yere ulaşılmalıdır ( \rm \psi ( \phi + 2 \pi ) = \Psi ( \phi) ). Bu nedenle; \rm \Psi m_l( \phi + 2 \pi) = \Big({1 \over 2 }\Big)^{1/2} e^{im_l( \phi + 2 \pi)} \qquad \qquad (Eşitlik \; 23 ) \rm \Psi m_l( \phi + 2 \pi) = \Big({1 \over 2 }\Big)^{1/2} e^{im_l \phi} e^{2 \pi im_l} \qquad \qquad (Eşitlik \; 24 ) \rm \Psi m_l( \phi + 2 \pi) = \Psi m_l ( \phi ) e^{2 \pi i m_l} \qquad \qquad (Eşitlik \; 25 ) Ayrıca \rm e^{i \pi} = -1 olduğundan; \rm \Psi m_l ( \phi + 2 \pi) = \Psi m_l ( \phi )(-1)^{2m_l} \qquad \qquad (Eşitlik \; 26 ) Bu nedenle \rm 2m_l herhangi bir pozitif ya da negatif tamsayı olabilir. Böylece; \rm m_l = 0, \; \pm 1, \; \pm 2, \; \pm 3, \; ... değerlerin' alabilir. Böylece dönme enerjisi \rm m_l 'ye bağlı olduğundan quantize olmuş bir enerjidir. \rm E_{ m_l } = { m_l ^2 \hbar^2 \over 2 I} \qquad m_l = 0, \; \pm 1, \; \pm 2, \; \pm 3, \; ... \qquad \qquad (Eşitlik \; 27 ) Enerji \rm m_l 'in karesine bağlı olarak değer aldığından \rm m_l 'nin işaretinden bağımsızdır. Elde edilen sonuçlar tek bir kütle merkezindeki dönme için türetilmiş olsada bir eksen etrafındaki dönme olayı içinde kullanılabilir. Ayrıca kuantum mekaniksel eşitlik ile Eşitlik 14 deki klasik eşitlik kullanılarak açısal momentumunda kuantize olduğunu söyleyebiliriz. Dönme enerjisi \rm E_{m_l}; \rm E_J= { m_l ^2 \; \hbar ^2 \over 2I } = { J_z^2 \over 2I } \qquad L= \hbar \;m_l \qquad m_l = 0, \; \pm 1, \; \pm 2, \; \pm 3, \; ... \qquad \qquad (Eşitlik \; 28 ) olarak elde edilir. Üç Boyuttaki Dönme Hareketi : r yarıçaplı bir küre yüzeyi üzerinde hareket eden bir parçacık düşünelim. Bu durumda ikinci dönme sınır şartı söz konusu olacaktır ki bu ikinci bir kuantum sayısının ortaya çıkması anlamını taşır. Bu nedenle dalga fonksiyonu \rm \Psi, biri \rm \theta ve diğeri \rm \phi olmak üzere iki açısal değişkene bağlı kısmi bir difransiyel eşitliktir. Bu nedenle \rm \Psi iki farklı eşitlikten meydana gelecektir \rm (\Psi = \Theta \Phi ). \rm \Theta; \rm \theta ' nın; \rm \Phi ; ise \rm \phi 'nin bir fonksiyonudur. Burada çözüm üzerinde durulmaksızın doğrudan ortaya çıkan sonuçlar verilecektir. \rm m_l, 'den sonra ortaya çıkan ikinci kuantum sayısı l dir. Üç boyuttaki kuantum sayılarının aldıkları değer; \rm l = 0, \; 1, \; 2, \; 3, \; ... \rm m_l = 0, \; \pm 1, \; \pm 2, \; \pm 3, \; ... dir. Ayrıca \rm m_l = l,\; l-1, \; l-2, \; l-3, \; ..., -l arasında değer alır. l, pozitif değerler alır ve l 'nin alınan değerleri için \rm m_l'nin değerleri \rm 2l+1 değerine izin verir. Parçacığın enerjisi E; \rm E=l(l+1){ \hbar ^2 \over 2I} \qquad l = 0, \; 1, \; 2, \; 3, \; ... \qquad \qquad (Eşitlik \; 29 ) sınırlı değerleri alabilir. Görüldüğü gibi enerji kuantizedir ve \rm m_l'den bağımsızdır. Bu nedenle \rm m_l 'nin değerlerinden biri için aynı enerji seviyesine karşı gelen 2l+1 farklı dalga fonksiyonu söz konusudur. Bu nedenle kuantum sayısı l 'nin herhangi bir değeri 2l+1 defa dejeneredir ( Örnek ) . Açısal Momentum : bir cismin dönme hareketi sırasında sahip olduğu hareket miktarını tanımlayan bir fiziksel büyüklüktür. Doğrusal momentumun (lineer momentumun) dönme hareketine uygulanmış hâli olarak düşünülebilir. \rm J = r \times p J = Açısal momentum (vektörel bir büyüklük) r = Cismin dönme merkezine uzaklığı p = Doğrusal momentum ( p = m V ) Açısal Momentumun Özellikleri Korunumu : Dışarıdan bir tork (moment) uygulanmadığı sürece, toplam açısal momentum korunur. Bu, dönme hareketinde bir sistemin sabit kalmasını sağlayan temel bir ilkedir. Örneğin, bir buz patencisinin kollarını kapattığında daha hızlı dönmesi bu ilkeye dayanır. Vektörel Büyüklük : Açısal momentum hem büyüklüğe hem de yön bilgisine sahiptir. Yönü, dönme eksenine dik olacak şekilde sağ el kuralıyla belirlenir.