| Ana Sayfa  | Dersler | Ders Programı | Simülasyonlar  | Diğer | İletişim |

Süper Pozisyonlar Ve Olası Değerler Schrödinger Eşitliğinin çözümü olarak dalga fonksiyonunu \rm \Psi = Ae^{ik \chi } + Be^{-ik \chi } olarak daha önce anlatmıştık \rm ^* . Serbest bir parçacık için dalga fonksiyonundaki katsayıların A = B olduğunu düşünelim. Böyle bir parçacığın lineer momentumu ne olacaktır? Operatör tekniğini kullanırsak, dalga fonksiyonunu \rm \Psi = A \big( e^{ik \chi } + e^{-ik \chi } \big) = 2ACosk \chi \qquad \qquad \qquad \qquad (Eşitlik \; 1 ) olup tam bir dalga fonksiyonudur. Eğer bu dalga fonksiyonuna momentum operatörünü uygularsak; \rm -i \hbar { d \Psi \over d \chi }= -2ikA \hbar{ d \over d \chi} (Cosk \chi) = 2ikA \hbar (Sink \chi) \qquad \qquad \qquad \qquad (Eşitlik \; 2 ) sonucu ile karşılaşırız. Eşitliğin sağ tarafından da görüldüğü gibi özdeğere sahip bir eşitlik değildir. Parçacığın dalga fonksiyonun, operatörün özfonksiyonu olmadığından özellik belirsizlik taşımaktadır. Bununla beraber, bu örnekte momentum tam olarak belirsiz değildir. Çünkü cosinüs dalga fonksiyonu lineer bir süperpozisyondur. \rm e ^{ik \chi} ve e ^{-ik \chi} değerlerinin kendi başlarına belirli momentum hallerine karşı geldiğini söyleyebiliriz. Sembolik olarak süperpozisyonları \rm \Psi = \Psi _{ \rightarrow } + \Psi _{ \leftarrow } \qquad \qquad \qquad \qquad (Eşitlik \; 3 ) şeklinde yazabiliriz. Bu dalga fonksiyonunun yorumunu, parçacığa momentumu ölçülebilirse, büyüklüğü \rm k \hbar olarak bulunabilir. Çünkü dalga fonksiyonunun herhangi bir bileşeni için olması gereken değerin böyle olması gerektiğini daha önce göstermiştik. Fakat ölçümlerin yarısı dalganın sağa diğer yarısı sola hareket ettiğini gösterecektir. Benzer yaklaşımları herhangi bir dalga fonksiyonuna uygulamak için bir süperpozisyon yazılır. Bu nedenle; dalga fonksiyonunu pekçok farklı lineer momentum eigen fonksiyonlarının bir toplamı olduğunu düşünürsek, dalga fonksiyonu; \rm \Psi = c_1 \Psi _1 + c_2 \Psi _2 + c_3 \Psi _3 + ... = \sum _i c_i \Psi _i \qquad \qquad \qquad \qquad (Eşitlik \; 4 ) şeklinde yazılabilir. Buradaki \rm c_i değerleri, sayısal katsayılar olup farklı momentum hallerine karşı gelen \rm \Psi _i için farklıdır. Böylece kuantum mekaniği ile aşağıdaki sonuçlara ulaşabiliriz. Momentum ölçüldüğünde, \rm \Psi _i ye karşı gelen değerlerden birinin süperpozisyona katkısı ölçülebilir. Bunların olası değerleri önceden söylenemez fakat bir seri gözlem sonucu ölçülen özel bir değerin olasılığı süperpozisyondaki katsayıların karesi ile orantılı olacaktır (Eğer c kompleks ise \rm c^*c olacaktır.). Daha fazla sayıdaki gözlemlerin ortalama değeri gözlemlerin olasılık değeri ile verilir \rm < A > = \int \Psi ^* \Psi d \tau. . Bu formül yalnızca normalize fonksiyonlar için doğrudur. Belirsizlik Prensibi: Eğer bir parçacığın dalga fonksiyonunu \rm Ae^{ik \chi} şeklindeyse, \rm k \hbar momentumu bir yöne doğru harekete karşı gelir. Bu durumdaki parçacığın yerinin neresi olduğunu bilmek isteyebiliriz. Born yaklaşımına göre bu sorunun cevabı dalga fonksiyonunun olasılık yoğunluğu hesaplanarak verilebilir. 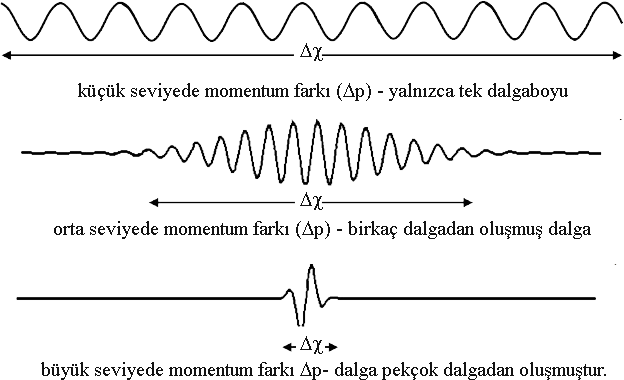Böylece; \rm \Psi ^* \Psi (Ae^{ik \chi})(Ae^{-ik \chi}) = A^2(e^{ik \chi})(e^{-ik \chi}) = A^2 \qquad \qquad \qquad \qquad (Eşitlik \; 5 ) yazılabilir. Buradan da görüldüğü gibi olasılık yoğunluğu \rm \chi 'den bağımsız sabit bir sayısıdır. Bu nedenle parçacık eşit olasılıkla herhangi bir yerde bulunabilir. Başka bir deyişle momentum kesin bir şekilde belirlenirse, parçacığın yerinin belirlenmesi imkansızdır. Heisenberg belirsizlik prensibinin bu parçası kuantum mekaniksel pekçok ünlü sonuçlarından biridir. "Aynı anda hassas bir şekilde momentum ve parçacığın yeri ölçülemez demektir." Prensibi daha fazla tartışmadan önce diğer yarısı üzerinde durmalıyız. Eğer parçacığın yerini tam olarak biliyorsak momentumu hakkında herhangi birşey söyleyemeyiz. Eğer parçacığın belli bir bölgede olduğunu biliyorsak, bu bölgede dalga fonksiyonu büyük değerlere sahipken diğer bölgelerde sıfır olmalıdır. Butip bir dalga fonksiyonu pekçok sayıdaki harmonik (cosinüs ve sinüs dalgası) ile ortaya çıkabilir. Bu dalgaların herbiri ise bir \rm e^{ik \chi } fonksiyonuna karşı gelecektir. Başka bir deyişle böylesine dar bir pik şeklinde ortaya çıkacak dalga fonksiyonu pekçok farklı lineer momentumdaki dalga fonksiyonlarının süper düzenlenmeleri sonucu ortaya çıkabilir (Şekil 1). Şekil 1 : Belirsizlik prensibine göre bir dalganın momentum ve yerindeki belirsizlik. Bu şekilde yönlenmiş sonsuz sayıda fonksiyon kullanılacak olursa, dalga fonksiyonu keskin, sonsuz derecede dar bir pik verir ki bu pik parçacığın yerinin tam olarak belirlenmesi anlamına gelir. Bu durumda parçacık tam olarak lokalize olmuştur fakat momentumunun ne olduğunu söylemeye gelince tam bir problem vardır. Bunun nedeni, ölçeceğimiz momentumun sonsuz sayıdaki dalga fonksiyonlarından birine ait olmasından kaynaklanır. Heisenberg yer ve momentumdaki belirsizlikle ilgili olarak \rm \Delta p \Delta \chi \ge \hbar/2 \qquad \qquad \qquad \qquad (Eşitlik \; 6 ) eşitliğini önerdi. Burada \rm \Delta p ; lineer momentumdaki belirsizlik olup ortalama değerden momentum sapmalarının karelerinin kareköküdür. \rm \Delta \chi ise; esas olarak ortalama pozisyondan pozisyon sapmalarının kareleri kareköküdür. Aslında süperpozisyonun yarı genişliğidir.