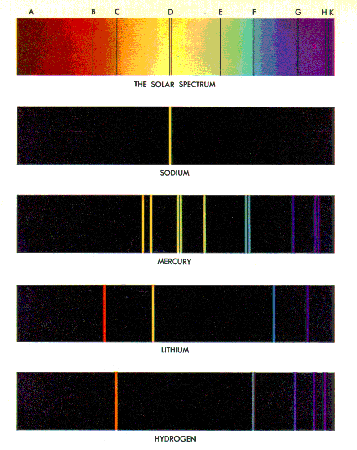
Atomik ve Moleküler Spektrumlar
Atomların ye da moleküllerin absorbe ettikleri veya yaydıkları radyasyonların frekansları gözlendiğinde enerjinin kuantize olduğuna dair direk kanıtları ele geçmeye başlar. Tipik bazı atomik spektrumlar Şekil 1'de verilmiştir.
Şekil 1 : Güneşin ve bazı elementlerin ışık spektrumları.
Bilindiği gibi Rutherfort atom modeli tarafından aydınlatılamamış noktalardan biri atomik spektrumlardaki kesikli çizgilerin varlığıydı. Bohr atom modelinde atomda elektronların dolaşabildiği belirli yörüngelerin varlığının kabulü ile birlikte bu çizgilerin nedeni de açıklandı. Bu teoriye göre;
Bir elektron çekirdek etrafında hareket ederken çekirdek ile elektron arasındaki Coulomb kuvvetil ile elektronun sahip olduğu merkezcil kuvvetin birbirine eşit olması gerekir. Aksi durumda elektron ya çekirdeğe düşmeli veya bulunduğu yöüngeden savrulup gitmelidir. Bu nedenle;
\rm F_{Coulomb}=F_{Merkezcil} \qquad \qquad (Eşitlik \; 1 )olmalıdır. Çekirdek ile elektron arasındaki Coulomb kuvvetinin büyüklüğü;
\rm F_{Coulomb}={ z q_e^2 \over 4 \pi \epsilon _o r^2} \qquad \qquad (Eşitlik \; 2 )ve merkezcil kuvvet büyüklüğü
\rm F_{Merkezcil} = { m \upsilon ^2 \over r} \qquad \qquad (Eşitlik \; 3 )dir. Burada, z; çekirdek yükü (proton sayısı), \rm q_e; elektronun yükü, \rm \epsilon _o ; boşluğun elektriksel geçirgenlik katsayısı, r; elektronun yörünge yarıçapı, m; elektronun kütlesi ve \rm \upsilon ; elektronun hızıdır.
Bu iki hız eşitlenirse;
\rm { z q_e^2 \over 4 \pi \epsilon _o r^2} = { m \upsilon ^2 \over r} \qquad \qquad (Eşitlik \; 4 )Yörüngedeki elektronun hızı ile ilgili;
\rm \upsilon ^2 = { z q_e^2 \over 4 \pi \epsilon _o mr} \qquad \Rightarrow \qquad \upsilon = \sqrt{ { z q_e^2 \over 4 \pi \epsilon _o mr}} \qquad \qquad (Eşitlik \; 5 )veya yörüngenin yarıçapı için;
\rm r = { z q_e^2 \over 4 \pi \epsilon _o m \upsilon ^2 } \qquad \qquad (Eşitlik \; 6 )Bu yörüngede dönen elektronun toplam enerjisi kinetik ve potasiyel enerjiden oluşacağından;
\rm E=E_{toplam}=E_{kinetik}+E_{potansiyel} \qquad \qquad (Eşitlik \; 7 )\rm E={1 \over 2} m \upsilon ^2 + (- { zq_e^2 \over 4 \pi \epsilon _o r} ) \qquad \qquad (Eşitlik \; 8 )Eşitlik 5 e göre \rm m \upsilon ^2 = { z q_e^2 \over 4 \pi \epsilon _o r} olacağında, Eşitlik 8;
\rm E={1 \over 2} { z q_e^2 \over 4 \pi \epsilon _o r} - { zq_e^2 \over 4 \pi \epsilon _o r} \qquad \qquad (Eşitlik \; 9 )\rm E= -{ z q_e^2 \over 8 \pi \epsilon _o r} \qquad \qquad (Eşitlik \; 10 )şeklinde yeniden düzenlenebilir.
Bohr tarafından öne sürülen şart elektronun açısal momentumunun \rm h/2 \pi 'nin tam katları olması gerekiyordu. Yani;
\rm L= m \upsilon r = { nh \over 2 \pi } \qquad \Rightarrow \qquad L= m \upsilon r = { n \; \hbar } \qquad ( n = 1,2,3, ...). \qquad \qquad (Eşitlik \; 11 )Buna göre elektronun hızı \rm \upsilon için;
\rm \upsilon = { n \hbar \over m r } \qquad \qquad (Eşitlik \; 12 )yazılabilir. Eşitlik 5 de bu hız büyüklüğü yerine konursa
\rm \upsilon ^2 = { n^2 \hbar ^2 \over m^2 r^2 } = { z q_e^2 \over 4 \pi \epsilon _o mr} \qquad \qquad (Eşitlik \; 13 )Böylece yörünge yarıçapı;
\rm r= { 4 \pi \epsilon _o \hbar ^2 \over m q_e^2} { n^2\over z} \qquad \qquad (Eşitlik \; 14 )olarak elde edilebilir. Bu denklem bize hidrojen atomuna benzer tek elektronlu atomların Bohr yarıçapını verir.
r değeri toplam enerji denklemi olan Eşitlik 10 da yerine konulursa;
\rm E=-{ z^2 q_e^4 m \over 8 \epsilon _o h^2 } {1 \over n^2} \qquad \qquad (Eşitlik \; 15 )ifadesi elde edilebilir.
İki enerji seviyesi arasındaki fark
\rm \Delta E = { z^2 m q_e^4 \over 8 \epsilon _o ^2 h^2} \Big( { 1 \over n_2 ^2 } - { 1 \over n_1 ^2 } \Big) \qquad \qquad (Eşitlik \; 16 )şeklinde bulunabilir. Ayrıca \rm E= h \nu veya E= \rm {h c \over \lambda } olduğundan;
\rm { 1 \over \lambda } = { z^2 m q_e^4 \over 8 \epsilon _o ^2 ch^3} \Big( { 1 \over n_1 ^2 } - { 1 \over n_2 ^2 } \Big) \qquad \qquad R= { m q_e^4 \over 8 \epsilon _o ^2 ch^3}=1.097 \times 10^7 \; m^{-1} \qquad \qquad \qquad (Eşitlik \;2)bağıntıları ile verilmiştir ( Örnek ). R; Rydberg sabiti olarak adlandırılır. de Broglie dalga bağıntısı kullanıldığında Bohr modelindeki açısal momentumun \rm h/2 \pi olma şartının nedeni kolayca anlaşılır.
Şekil 2 : Bir çekirdek etrafındaki elektrona eşlik edemeycek ve elektrona eşilik edebilecek dalga örneği.
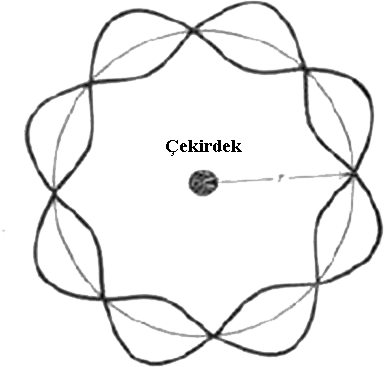
Elektronun belirli bir yörüngede kalabilmesi için yaptığı dalga hareketinin dalga boyunun tam katlarının yörüngenin çevresine eşit olması gerekir. Eğer yörünge tam sayıda dalga içermezse dalgalar birbirlerini yok ederler (Şekil 2). Böyle bir sonuç ise ancak elektronun yörüngede bulunmaması ve elektronun yok olması anlamına gelir. Bu açıklamalara göre;
\rm n \lambda = 2 \pi r\rm n { h \over m \upsilon } = 2 \pi r\rm m \upsilon r = { nh \over 2 \pi } = n \; \hbareşitliği elde edilebilir ki bu Bohr'un açısal momentum şartı ile aynıdır. ( Örnek )
Kaynaklar |
