| Ana Sayfa  | Dersler | Ders Programı | Simülasyonlar  | Diğer | İletişim |

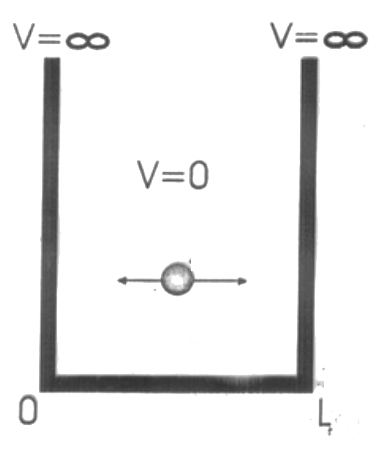
Tek Boyutlu Kutu İçindeki Parçacık Eğer serbestçe hareket eden bir tanecik tek boytlu bir kutu içerisine konulmuş olsa parçacığın dalga fonksiyonunda acaba bir değişiklik meydana gelecek midir? Bu sorunun cevabını bulabilmek için bu m kütleli parçacığın L tek boyutlu bir kutu içerisine hapsedildiğini düşünelim. Bu parçacığın potansiyel enerjisinin kutu içerisinde sıfır ve kutu duvarlarında sonsuz olduğunu düşünelim (Şekil 1). Şekil 1 : L uzunluğunda bir boyutlu kutu. içindeki tanecik problemi. Taneciğin duvarlar üzerindeki potansiyel enerjisi sonsuz, kutu içerisindeki potansiyel enerjisi ise sıfırdır. Duvarlar arasındaki bölgede taneciğin potansiyel enerjisi V=0 olduğundan Schrödinger Eşitliği; \rm - { \hbar \over 2m }{ d^2 \Psi \over d \chi ^2} =E \Psi \qquad \qquad (Eşitlik \; 1 ) ve genel çözümünün de \rm E={ k^2 \hbar ^2 \over 2m} \qquad \qquad (Eşitlik \; 2 ) olduğu söylemiştik. Aynı çözüm kutu içerisindeki tanecik içinde geçerli olur mu? Bu kutu içerisindeki tanecik kutu cidarlarındaki yüksek potansiyel enerjiye sahip olduğundan prçacığın dalga fonksiyonu duvarlar üzerinde sıfır olmalıdır. Bir başka deyişle parçacık duvarlar üzerinde bulunamayacaktır ve elbette taneciğin bu kutu içerisinde bulunduğundan emin olmalıyız. \rm \Psi dalga fonksiyonunun çözümünü \rm \Psi = Ae^{ik \chi} + Be^{-ik \chi} \qquad e^{ik \chi}=Cos k \chi +iSin k \chi \qquad k= \Big( {2mE \over \hbar ^2 } \Big)^{ 1/2 } \qquad \qquad (Eşitlik \; 3 ) şeklinde vermiştik. Ancak tanecik kutu içerisine konulduğunda duvarlar üzerinde ( \rm \chi = 0 \; ve \; \chi = L , ) sınırlayıcı şartlar nedeni ile \rm \Psi(0)=0 \; ve \; \Psi(L)=0 olmak zorundadır. Bu nedenle Eşitlik 3 'e göre A+B=0 olmalıdır. Buda A=-B demektir. Bu nedenle eşitlik; \rm \Psi. = A(e^{ i k \chi} - e^{ -i k \chi}) \qquad \qquad (Eşitlik \; 4 ) \rm \Psi = 2iASink \chi = A' Sink \chi \qquad \qquad (Eşitlik \; 5 ) şeklinde yazılabilir. Bu nedenle tek boyutlu kutudaki tanecik için Schrödinger eşitliği \rm \Psi = A'Sin \Big( {2mE \over \hbar ^2} \Big)^{1/2} \chi \qquad \qquad (Eşitlik \; 6 ) şeklindedir. Ayrıca parçacık kutu içerisinde bulunduğundan; \rm \int _0 ^L \Psi ^* \Psi d \chi = (A')^2 \int _0 ^L Sin^2 k \chi d \chi = 1 \qquad \qquad (Eşitlik \; 7 ) \rm \int _0 ^L \Psi ^* \Psi d \chi = {(A')^2 \over 2 } \int _0 ^L (1-Cos2k \chi ) d \chi = 1 \qquad \qquad (Eşitlik \; 8 ) \rm \int _0 ^L \Psi ^* \Psi d \chi = {(A')^2 \over 2 } L = 1 \qquad \qquad (Eşitlik \; 9 ) \rm A'=\pm \sqrt{ 2 \over L } \qquad \qquad (Eşitlik \; 10 ) olarak bulunabilir. Böylece genel çözüm için A' katsayısının + işaretli çözümü kullanılabilir. Tek boyutlu kutudaki tanecik için Schrödinger eşitliği böylece \rm \Psi = \sqrt{ 2 \over L } Sin \Big( { 2mE \over \hbar ^2 } \Big) ^{1/2} \chi \qquad \qquad (Eşitlik \; 11 ) şeklinde yazılabilir. Şimdi kutunun diğer ucundaki ( \rm \chi = L) sınır şartı göz önünde bulunduralım. Bu noktada \rm \Psi(L)=0 olmak zorunda olduğundan, ve \rm \sqrt {2 \over L} =0 olamayacağından ,Bu ancak \rm \Big( { 2mE \over \hbar ^2} \Big) = \pm n \pi \qquad n=1,2,3,... \qquad \qquad (Eşitlik \; 12 ) olması ile gerçekleşebilir. Bu durumda taneciğin enerjisi \rm E={ h^2 n^2 \over 8mL^2} \qquad \qquad (Eşitlik \; 13 ) olacaktır. Bu sonuca göre; serbest bir tanesik herhangi bir enerji değerine sahip olabilirken kutu içerisinde bulunan bir taneciğin enerjisini kuantize olduğunu görmekteyiz. Komşu enerji seviyeleri arasındaki fark \rm \Delta E=E_{n+1}-E_n=(2n+1){ h^2 \over 8mL^2} \qquad \qquad (Eşitlik \; 14 ) dir. Bu fark kabın uzunluğuna bağlı olarak azalır ya da artar ve eğer kap çok büyükse \rm \Delta E = 0 olur. Laboratuvar boyutlarındaki bir kapta atomlar ya da moleküller serbestçe hareket ederler ve bu nedenle öteleme enerjisi kuantize değildir. Tek boyutlu kutudaki tanecik için dalga fonksiyonu \rm \Psi = \sqrt{2 \over L }Sin{ n \pi \over L} \chi \qquad \qquad (Eşitlik \; 15 ) şeklindedir. Ayrıca n = 0 değeri olmadığından en düşük enerjili durumdaki tanecik \rm E={ h^2 \over 8mL} \qquad \qquad (Eşitlik \; 16 ) enerjisine sahiptir. Bu en düşük enerji seviyesi sıfır noktası enerjisi olarak adlandırılır. Sıfır noktası enerjisinin hareket noktası iki yolla açıklanabilir. Belirsizlik prensibine göre; sonlu bir bölgeye hapsedilmiş bir parçacığın kinetik enerjisinin olması gerekir. Bunun nedeni, parçacığın yerinin tam olarak belirlenememesi ve momentumunun sıfırdan farklı olmasından kaynaklanır. Eğer dalga fonksiyonu duvarlarda sıfır fakat devamında düzgün olarak değişen ve bu nedenle her noktada sıfır olmadığına göre eğriseldir. Bir dalga fonksiyonunun eğriselliği kinetik enerjisinin olmasını gerektirir. Bu iki neden de sıfır noktası enerjisinin olması gerekliliğini gösterir. Tek Boyutlu Kutu İçindeki Parçacığın Yoğunluğu Dalga fonksiyonunun anlamını tartışırken Bir parçacığın dalga fonksiyonunun genliği \rm \chi noktası civarında \rm \Psi ise, \rm \chi ve \rm \chi + d \chi arasında parçacıkların bulunma olasılığının \rm \Psi ^* \Psi d \chi olduğunu söylemiştik. Şekil 2 : Tek boyutlu kutu içinde parçacığın \rm \chi nin değişimi ile \rm \Psi ve \rm \Psi ^2 nin dağılımı. n. enerji seviyesindeki taneciğin lineer momentumu \rm p _\chi ^2 = 2mE_n \qquad \qquad (Eşitlik \; 17 ) olacağından; \rm p _\chi = \pm { nh \over 2L} \qquad \qquad (Eşitlik \; 18 ) yazılabilir. 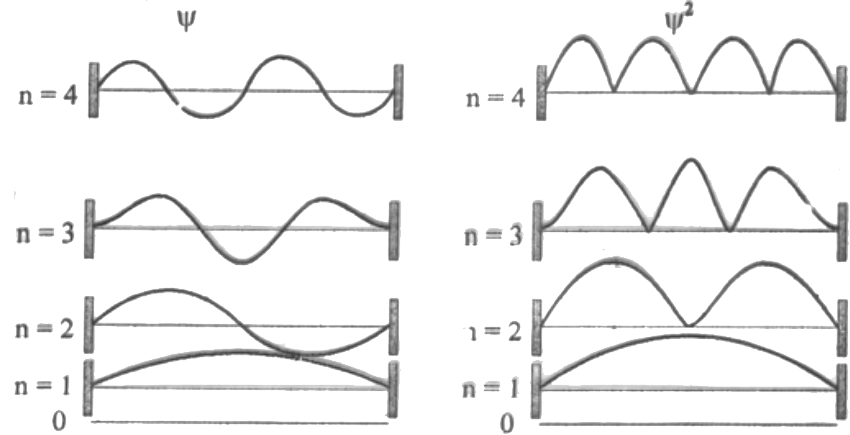Bir de Broglie dalgası için \rm \lambda = h/ p _\chi olduğundan \rm L= n { \lambda \over 2 } ifadesi elde edilebilir. Bu son ifadeden de görüldüğü gibi L uzunluğundaki kutu içerisine \rm \lambda /2 'nin tam katlarının sığmak zorunda olduğunu göstermektedir. n 'in farklı değerleri için \rm \Psi ve \rm \Psi ^2 L uzunluğundaki kutudaki durumu Şekil 2'de görülmektedir (Örnek). Üç Boyutlu Kutu İçindeki Parçacık Şimdi parçacığın üç boyutlu bir kutu içerisinde olduğunu düşünelim. Bu durumda parçacık \rm L_\chi, \; L_y \; ve \; L_y kenar uzunluğuna sahip dikdörtgenler prizması şeklindeki bir bölgede hareket eder. Tek x boyutlu kutuda geçerli olan şartların bu kutu içinde geçerli olduğunu düşünelim. Bu durumda Schrödinger Eşitliği; \rm -{ \hbar \over 2m } \Big( { \partial ^2 \over \partial \chi ^2} + { \partial ^2 \over \partial y ^2} + { \partial ^2 \over \partial z ^2} \Big) \Psi = E \Psi \qquad \qquad (Eşitlik \; 19 ) olacaktır. Bu eşitlik içinde çözüm şekli biraz daha farklı da olsa tek boyutlu kutudaki çözüme benzer sonuçlar elde edilir. Fakat burada bu ayrıntılara girilmeksizin sonuçlar verilecektir. Herbir eksen için dalga fonksiyonu \rm \Psi_{ ( \chi ) } = \pm \sqrt{ 2 \over L_\chi} Sin \Big( { n _\chi \pi \chi \over L_\chi } \Big) \qquad \qquad (Eşitlik \; 20 ) \rm \Psi_{ ( y ) } = \pm \sqrt{ 2 \over L_y} Sin \Big( { n _y \pi \chi \over L_y } \Big) \qquad \qquad (Eşitlik \; 21 ) \rm \Psi_{ ( z ) } = \pm \sqrt{ 2 \over L_z} Sin \Big( { n _z \pi \chi \over L_z } \Big) \qquad \qquad (Eşitlik \; 22 ) şeklindedir. Parçacığın üç boyuttaki dalga fonksiyonu \rm \Psi = \Psi _\chi \Psi _y \Psi _z dir. Bu nedenle parçacığın dalga fonksiyonu \rm \Psi = \pm \sqrt{ 8 \over L_\chi L_y L_z } \Big[ Sin \Big( { n _\chi \pi \chi \over L_\chi } \Big) Sin \Big( { n _y \pi \chi \over L_y } \Big) Sin \Big( { n _z \pi \chi \over L_z } \Big) \Big] \qquad \qquad (Eşitlik \; 23 ) dur. Taneciğin enerjisi ise herbir boyuttaki enerjilerinin toplamı olacağından \rm \rm E= E _\chi + E_y + E_z \; olacağından; \rm E= { n _\chi ^2 h^2 \over 8mL_\chi ^2 } + { n _y ^2 h^2 \over 8mL_y ^2 } + { n _z ^2 h^2 \over 8mL_z ^2 } \qquad \qquad (Eşitlik \; 24 ) dir. Eğer parçacık L uzunluğuna sahip küp şeklindeki bir alanda hareket ediyorsa sahip olduğu enerji \rm E={ h^2 \over 8mL^2 } \big( n_\chi ^2 + n_y ^2 + n_z ^2 ) \qquad \qquad (Eşitlik \; 25 ) kadardır ( Örnek ).