| Ana Sayfa  | Dersler | Ders Programı | Simülasyonlar  | Diğer | İletişim |

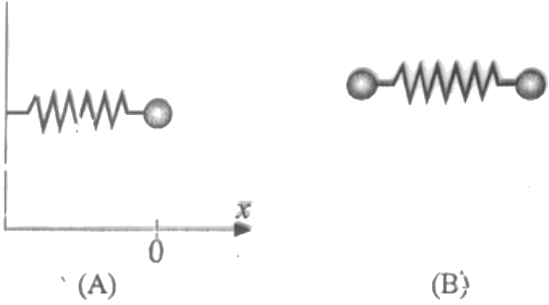
Titreşim Hareketi Klasik Harmonik Osilatör Molekülerin titreşimlerini anlamak için harmonik bir osilatörün kuantum mekaniksel davranışlarını anlamamız gerekir. Bu nedenle harmonik bir osilatörün klasik davranışını gözden geçirmemiz gerekir. Harmonik osilatörün en basit örneği ağırlıksız bir ortamda ideal bir yay ile duvara tuturulmuş bir yaydır (Şekil 1). Şekil 1 (A)'da görüldüğü gibi, kütle \rm \chi ekseni üzerinde hareket eder ve koordinat sisteminin orgini denge pozisyonu olarak alınmıştır. Şekil 1 : (A) Ağırlıksız bir ortamda yayla duvara tuttturulmuş m kütlesi. Kütlenin denge pozisyonu \rm \chi = 0 Bu kütle denge pozisyonu civarında titreşir bu hareket harmonik olarak adlandırılır. Eğer bu kütleye F kuvveti uygulanırsa \rm \chi orijinden ayrılma miktarı olmak üzere; \rm F= - k \chi \qquad \qquad (Eşitlik \; 1 ) eşitliği yazılabilir. Negatif işareti F 'in \rm \chi 'deki yer değiştirmeye zıt olmasından kaynaklanmaktadır. Orantı sabiti k, kuvvet sabiti olarak adlandırılır. k 'nın değeri zayıf yaylar için küçük, sert yaylar için büyüktür. \rm \chi yönündeki hareket için aynı zamanda \rm m { d^2 \chi \over dt^2} + k \chi = 0 \qquad \qquad (Eşitlik \; 2 ) yazılabilir. Bu eşitliğin genel çözümü Schrödinger çözümününe benzer. \rm \chi (t) = ASin \omega t + BCost \omega t \qquad \qquad (Eşitlik \; 3 ) Buradaki \rm \omega = (k/m)^{1/2} olup, saniyede radian olarak temel titreşim frekansıdır. Eğer yayı \rm \chi _o noktasına kadar çeker ( \rm \chi _o noktasında kütle hareketsizdir.) ve sonra bırakılırsa hareketin zamanla değişimi; \rm \chi (t) = \chi _o Cos t \omega t \qquad \qquad (Eşitlik \; 4 ) eşitliği ile verilir. Kütle, saniyede \rm \omega radian frekansta veya saniyede \rm \nu = \omega / 2 devir ile \rm + \chi _o \; ve \; - \chi _o arasında salınır. Bu harmonik osilatörün enerjisi kinetik ve potansiyel enerjisinin toplamına eşittir. Kütle \rm + \chi_o \; ve \; - \chi_o \; da olduğunda yalnızca potansiyel enerjiye sahipken \rm \chi = 0 da enerjisinin tümünü kinetik enerji oluşturur. Potansiyel enerji kuvvetin potansiyel enerjisinin kütlenin bulunduğu yere göre negatif türevi olmasından harekete hesaplanabilir ( \rm F= -dV/d \chi ). \rm V=- \int Fdx + sbt \qquad \qquad (Eşitlik \; 5 ) Ayrıca Eşitlik 1 göz önünde bulundurulur ve \rm \chi = 0 olduğu durum için sabitin sıfır olması gerektiği dikkate alınırsa \rm V= { k \chi ^2 \over 2} \qquad \qquad (Eşitlik \; 6 ) yazılabilir. Eşitlik 4'deki \rm \chi değeri eşitlikte yerine konulursa \rm V= { k \chi _o ^2 \over 2 } Cos ^2 \omega t \qquad \qquad (Eşitlik \; 7 ) elde edilebilir. Bu nedenle harmonik bir osilatörün potansiyel enerjisi sıfır ile \rm k \chi _o ^2 /2 arasında yer alacaktır. Hareket eden kütlenin kinetik enerjisi; \rm E_k = {1 \over 2} m \Big( { d \chi \over dt } \Big) \qquad \qquad (Eşitlik \; 8 ) dır. Eşitlik 4 ve ve \rm \omega = (k/m)^{1/2} olduğundan kinetik enerji için; \rm E_k= { 1\over 2 }m \omega^2 \chi _o ^2 Sin ^2 \omega t \qquad \qquad (Eşitlik \; 9 ) \rm E_k= { 1\over 2 }k \chi _o ^2 Sin^2 \omega t \qquad \qquad (Eşitlik \; 10 ) yazılabilir. Bu nedenle toplam enerji için \rm E=E_k + V = { 1\over 2 }k \chi _o ^2 Sin^2 \omega t + { 1\over 2 }k \chi _o ^2 Cos^2 \omega t \qquad \qquad (Eşitlik \; 11 ) \rm E={ 1 \over 2} k \chi _o ^2 \qquad \qquad (Eşitlik \; 12 ) yazılabilir. Bu nedenle toplam enerji sabitir. Kinetik enerji ile potansiyel enerji sıfır ile \rm k \chi _o ^2 /2 arasında değişir. Sonuç olarak toplam enerji kinetik enerji ile potansiyel arasında dönüşüme uğrar. Şekil 1 (B)'de görüldüğü gibi bir yaya bağlı iki kütle içinde benzer eşitlikler yazılabilir. Fakat buradaki eşitliklerde tek kütle yerine, iki kütle söz konusu olduğundan eşitliklerdeki kütlenin bulunduğu yere indirgenmiş kütlenin kullanılması gerekir. İndirgenmiş kütle \rm \mu ; \rm { 1 \over \mu } = { 1 \over m_1 } + { 1 \over m_2 } \qquad \qquad (Eşitlik \; 13 ) eşitliği ile tanımlanır. Bu nedenle diatomik molekülerdeki titreşim hareketi için \rm \omega = \Big( { k \over \mu} \Big)^{1/2} \qquad \qquad (Eşitlik \; 14 ) \rm \nu = {1 \over 2 \pi} \Big( { k \over \mu} \Big)^{1/2} \qquad \qquad (Eşitlik \; 15 ) eşitliği elde edilir ( Örnek 1, Örnek 2 ). Kuantum Mekaniksel Harmonik Osilatör \rm \mu kütleli kuantum mekaniksel harmonik osilatörün enerji seviyelerini elde etmek için klasik harmonik osilatör için kullanılan Hamiltonian fonksiyondan \rm H={ p _\chi ^2 \over 2 \mu } + { 1 \over 2 } \omega ^2 \mu \chi ^2 \qquad \qquad (Eşitlik \; 16 ) hareket etmek gerekir. Fakat kuantum mekaniksel Hamiltonian operatörün elde edilmesi için \rm P_\chi \; yerine \; p \chi = -i \, \hbar d / d \chi kullanılmalıdır. Böylece; \rm H= - { \hbar ^2 \over 2 \mu } { d^2 \over d \chi^2 } + 2 \pi ^2 \nu ^2 \mu \chi ^2 \qquad \qquad (Eşitlik \; 17 ) Şekil 2 : Şekil II. 4: (A) Klasik harmonik bir osilatör için potasiyel enerji eğrisi (B) Kuantum mekaniksel harmonik osilatör için izin verilen enerji seviyeleri ve dalga fonksiyonları (C) kuantum mekaniksel harmonik osilatör için olasılık yoğunluk fonksiyonu yazılabilir. Schrödinger eşitliğin çözümü şimdi tartışılmayacaktır. Fakat çözümün sonucu; \rm E_s = \Big( s + {1 \over 2 } \Big) h \nu _o \qquad \qquad s = 0, 1, 2, ... \qquad \qquad (Eşitlik \; 18 ) şeklinde verilir. 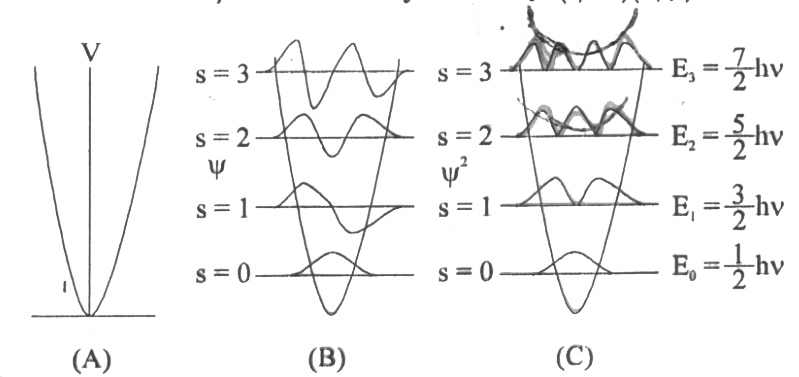s; titreşim kuantum sayısıdır ve; \rm \nu _o = {1 \over 2 \pi} \Big( {k \over \mu } \Big) ^{1/2} \qquad \qquad (Eşitlik \; 19 ) dir. Enerji seviyeleri \rm h \nu kadar birbirlerinden ayrılmıştır. Ayrıca temel durum için titreşim enerjisi sıfır değildir ve \rm h \nu /2 değerine sahiptir. Bu sıfır noktası enerjisi olarak adlandırılır. Bu kuantum mekaniksel sonucun en önemli noktası çekirdek hareketlerinin hiçbir zaman durdurulamayacağıdır. Mutlak sıfır noktasına gelindiğinnde dahi çekirdekler sıfır noktası hareketini yapmayı sürdürürler. Bu hareket Heisenberg belirsizlik prennsibinin doğal bir sonucudur. İlk iki enerji seviyesi için dalga fonksiyonu; \rm \Psi _o = \Big( { \alpha \over \pi } \Big)^{1/4} e^{ \alpha \chi^2 /2} \qquad \alpha = \Big( { k \mu \over \hbar^2 } \Big)^{}1/2 \qquad \qquad (Eşitlik \; 20 ) \rm \Psi _1 = \Big( { 4 \alpha ^3 \over \pi } \Big)^{1/4} \chi e^{ \alpha \chi^2 /2} \qquad \alpha = \Big( { k \mu \over \hbar^2 } \Big)^{}1/2 \qquad \qquad (Eşitlik \; 21 ) Temel hal için dalga fonksiyonu Gaussian olasılık fonksiyonu şeklindedir. Klasik Harmonik Osilatör ile Kuantum Mekaniksel Harmonik Osilatör Arasınndaki Farklar Klasik Harmonnik osilatörden farklı olarak kuantum mekaniksel harmonik osilatörü enerjisi kuantize olmuştur. Minimum enerji kuantum mekaniksel osilatör için kesinlikle sıfır değildir. Bu değer \rm {1 \over 2} h \nu 'ye eşittir. Kuantize enerji seviyeleri birbirlerinnden eşit üzaklıktadırlar ve iki enerji seviyesi arasındaki fark \rm h \nu kadardır. Kuantum mekaniksel harmonik osilatörün hareketi titreşim dalga fonksiyonu ile gösterilir. Bu dalga fonksiyonları yardımı ile titreşim enerji seviyeleri arasınndaki geçişlerinn ihtimalleri hesaplanabilir. Dalga fonksiyonunun karesi titreşim (titreşimsel) ihtimal fonnksiyonu olarak bilinir. Bu fonksiyon belirli bir anda çekirdekler arası uzaklığın belirli bir değerde olmasını gösterir. Seviyeleri gösteren çizgilerle eğrinin uç noktaları sistemin enerjisinin sadece potansiyel enerjiye eşit olduğu noktalardır. 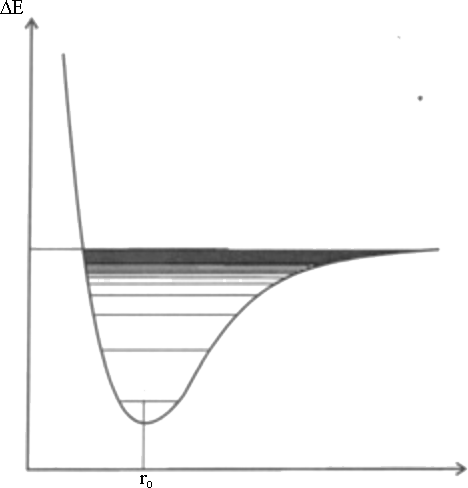Şekil 3 : Anharmonik osilatörde enerji seviyeleri. Anharmonik Osilatör İki atom birbirinden uzaklaştığı zaman birbirlerine bağlayan bağda bir gerilme meydana getirirler. Bunun sonucunda bağ kuvvetinde bir azalma meydana gelir. Bu nedenle de potansiyel enerji harmonik osilatörde olduğu gibi hızla değil yavaş yavaş artar ve sonuçta limit bir değere ulaşır. Bu limit değer molekülün dissosiyasyon enerjisidir. Yani sonuçta kimyasal bağ kopar ve atomlar birbirlerinden uzaklaşırlar. Aksine atomlar birbirlerine çok yaklaşmaya başlarsa elektron bulutu itmeleri artar ve bu nedenlede potansiyel enerjide hızlı bir artış meydana gelir. Anharmonik osilatörün bir diğer özelliği enerji seviyelerinin eşit aralıklı olmamasıdır. Titreşim kuantum sayıları arttıkça titreşim enerji değerleri birbirlerine yaklaşırlar. Sonuçta sürekli bir hal alırlar. Karmaşık moleküllerde çok boyutlu grafikler ortaya çıkar. Bu nedenle grafiklerin incelemeleri giderek zorlaşır. Bundan kurtulabilmek için karmaşık yapıdaki molekülün ağırlık merkezinde bulunan ve kütlesi molekülün indirgenmiş kütlesine eşit olarak kabul edilen tek bir taneciğn hareketine indirgenerek incelemeler sürdürülür.