| Ana Sayfa  | Özgeçmiş | Çalışmalar | Dersler | Ders Programı | Simülasyonlar  | Diğer | İletişim |

Bohr Atom Modeli

Niels Hendrik Bohr, Rutherford Atom Modeli ile Planck'ın Kuantum Teorisini kullanarak 1913 yılında yeni bir atom modeli öne sürdü. Bu yeni model Rutherford modelinin açıklayamadığı noktalara ışık tutuyordu. Bohr'un atom teorisi 3 temel varsayıma dayanır. Bir atomda bulunan her elektron çekirdekten ancak belirli uzaklıklardaki yörüngelerde bulunabilir. Her yörünge belirli bir enerjiye karşı gelir ve elektron yörüngelerden birinde hareket ederken enerji kaybederek çekirdeğe doğru yaklaşmaz. Yüksek enerji düzeyinde bir elektron düşük enerji düzeyine inerse enerji düzeyleri arasındaki enerji farkına eşit enerji yayınlanır. Elektronlar çekirdek çevresinde dairesel yörüngeler izlerler ve elektronların açısal momentumları ancak belirli değerler alabilirler. Bu değerler Planck Sabiti h ye bağımlı değerler alır. Bu yaklaşımlarla Bohr spektrumlardaki çizgileri ve Rutherford atom teorisinin açıklayamadığı diğer noktaları açıklamayı başardı. Bohr Yörüngelerinin Yarıçapı Bohr'un bu modeli H atomu, He+, Li+2, Be+3 iyonları gibi tek elektronlu sistemlerin spektrumlarını kolayca açıklayabilmektedir. Bu tip türlerin atomik yarıçaplarının ne kadar olduğunu hesaplayalım. Elektron atom çekirdeği etrafında hareket ederken Coulomb Çekme Kuvveti ve merkezkaç kuvveti etkisi altındadır. Elektron sürekli aynı yörüngeyi izlediğine göre bu iki kuvvet birbirine eşit olmalıdır. \rm {Ze^2 \over r^2 } = {mv^2 \over r } (1) yukarıdaki eşitlikten r değeri \rm r = {Ze^2 \over mv^2 } (2) olarak elde edilebilir. Ayrıca Bohr varsayımına göre bir elektronun açısal momentumu (mvr), \rm h / 2\pi nin katlarına bağlı değerler alacaktır. \rm mvr = n {h \over 2 \pi } (3) olup buradan v; \rm v = {nh \over 2 \pi mr } (4) kadar olacaktır. Son bağıntı; 2 nolu bağıntıda yerine konursa; \rm r = {n^2h^2 \over 4 \pi^2 mZe^2 } (5) bağıntısı elde edilir. Bohr Yörüngelerinin Enerjisi Atom çekirdeği etrafında dairesel yörüngelerde hareket eden elektronlar kinetik ve potansiyel enerjilere sahiptirler. Bu nedenle çekirdek etrafındaki elektronun enerjisi için; \rm E_T = {1 \over 2} mv^2 + \Big( - { 1 \over 4\pi \varepsilon_o } { Ze^2 \over r } \Big) (6) CGS sisteminde \rm { 1 \over 4\pi \varepsilon_o } = 1 olduğundan; \rm E_T = {1 \over 2} mv^2 + \Big( - { Ze^2 \over r } \Big) (7) yazılabilir. (1) nolu denklem hatırlanacak olursa; \rm mv^2 = { Ze^2 \over r } (8) ifadesi yazılabilir. Bu da 7 nolu eşitlikte yerine konulacak olursa \rm E_T = { 1 \over 2} { Ze^2 \over r } + \Big( - { Ze^2 \over r } \Big) = - { Ze^2 \over 2r } (9) elde edilebilir. (5) nolu eşitlikteki r yerine konursa \rm E_n =E_T = - { 2 \pi^2Z^2e^4m \over n^2h^2 } (10) ifadesi elde edilebilir. Bu formül n nin çeşitli değerleri için elektronların bulundukları enerji seviyesinde sahip olabilecekleri toplam enerjiyi verir. Bohr'un ikinci varsayımını hatırlarsak elektronun enerji seviyesini değiştirmesi sırasında kaybedeceği enerji \rm \Delta E = h \upsilon = E_s - E_i (11) kadar olacaktır. Böylece 10 nolu denklemi kullanarak atomdan yayılan radyasyonun dalga boyu veya atom tarafından yutulacak dalga boyu kolayca hesaplanabilir. Dalga sayısı \rm 1/ \lambda = \upsilon /c olduğu söylersek Hidrojen atomu için; \rm { 1 \over \lambda } = {2 \pi^2 me^4 \over ch^3 } \Big( {1 \over n_s^2} - {1 \over n_i^2} \Big) (12) yazılabilir. Burada \rm {2 \pi^2 me^4 \over ch^3 } Rydberg sabiti (R) olarak gösterilir ve değeri 109677,581 \rm \pm 0.007 cm-1 dir. Bohr Teorisinin Eksik Tarafları Bohr Modeli, Rutherforad Atom Modeline göre oldukça üstün tarafları olsa da bu kuramında eksik yönleri söz konusudur. Elektronun, maddesel nokta şeklinde düşünüldüğünden, yörünce üzerinde enerji yayımlamadan dönüşleri, yörüngeden yörüngeye atlayışı ve açığa çıkan enerjinin ışıma halinde alınıp verilmesi açıklanması kolay olmayan bir durumdur. Bohr atom modeli yalnızca tek elektronlu sistemlerin spektrumlarını açıklayabilir. Ve çok elektronlu sistemlerin spektrumları açıklamakta yetersiz kalır. Çok elektronlu atomların spektrumlarında enerji düzeylerinin herbirinin iki ya da daha fazla düzeye ayrıldığı görülmektedir. Yine hidrojen gazı, bir elektrik alanı veya magnetik alanda soğurma spektrumları incelenirse, enerji düzeylerinin çok elektronlu sistemlerde olduğu gibi iki ya da daha fazla enerji düzeyine ayrıldığı görülür. Bu konular Bohr Atom Teorisi tarafından açıklanamazlar. Bohr Atom Teorisi İle İlgili Etkileşimli Sorular Hidrojen Benzeri atomlarda enerji seviyeleri ve elektroik geçiş sırasında yayılan veya soğrulan dalgaboyu Siyah Cisim Işıması Bir madde yüksek sıcaklığa çıkartıldığında radyasyon yayar. Örneğin kızdırılmış bir metal çubuk kızarır. Bu olayın nedeni ısı uyarmaları sonucu cismin yüzey kısmında bulunan elektrik yüklerinin ivme kazanması ve elektromanyetik dalga yayması şeklinde anlatılır. Klasik fizik kuramına göre; ivmeli hareket eden elektrik yükleri elektromanyetik dalga yayar. Farklı değerde ivmelerin oluşturduğu ısı ışıması bu bölge için geçerli tüm dalga boyu şeridini içerir. Bu modele göre; birim yüzeyin yaydığı güç, cismin mutlak sıcaklığı ile orantılıdır. 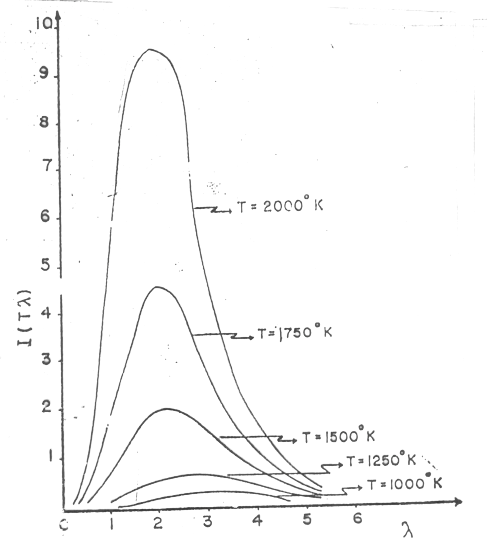Bu olayı 1897 de Stefan \rm I(T) = e\sigma T^4 (1) eşitliği ile vermiştir. Burada I(T); bir saniye içinde 1 cm2 lik yüzeyden bütün frekanslarda yapılan enerji ışımasını gösterir. e; yayın katsayısı olup 0 ile 1 arasında cismin özelliğine bağlı olarak değer alır. \rm \sigma ;Stefan-Boltzmann Sabiti olup değeri 5.6704x10-5 erg cm-2 s-1 K-4 dir. Şekil 1 de görüldüğü gibi siyah cisim ışımasına ait olan eğriler ve eğrilerin maksimum değerleri dalga mekaniği tarafından doğrulanamamış ya da farklı nitelikte bulunmuştur. Şekil 1 :Siyah cisim ışımasında dalga boyuna göre yayılan radyasyonların şiddetinin değişimi. Dalga teorisine göre; monokromatik ışıma ile taşınan enerji, bu ışımayı oluşturan sinüzodial dalganın genliğinin karesi ile orantılı olarak değişir. Bu düşüncenin parelelinde, polikromatik radyasyon ile taşınan enerji dalga boyu azaldığında sürekli bir artış göstermelidir. Oysa bu sonuç deneysel bulgulara ters düşmektedir. Bu nedenle Siyah Cisim Işıması dalga mekaniği yardımı ile açıklanamamaktadır. Nitekin Plack, ilerleyen sinüzodial bir dalga görünümü alan monokromatik radyasyonda, enerji kuantlar halide taşınmaktadır. hipotezi ile deneysel sonuçları açıklamakta büyük katkı göstermiştir. Herbir kuantumun enerjisi \rm E = h \upsilon (2) bağıntısı ile belirlidir. Burada h; Planck Sabiti, \rm \upsilon ; monokromatik radyasyonun frekansıdır. Deneysel sonuçların Planck Teorisi ile açıklanması şöyle yapılabilir. Radyasyonun dalga boyu azaldığı zaman herbir kuantumun enerjisi de artar. Fakat radyasyon ile taşınan kuantum sayısı azalır ve giderek sıfıra uzanır. Bir yüzeyin soğurganlık katsayısı ( a ) yüzey tarafından soğrulan enerjinin yüzeye düşen toplam enerjiye oranı olarak belirlenir. Termodinamik düşünceler ile bu iki katsayının eşit olduğu (e = a ) gösterilebilir. Bir cisim üzerine düşen bütün ışınları soğurma özelliği gösteriyorsa siyah cisim adını alır. Böyle bir cismin soğurganlık katsayısı a = 1 dir. Soğurma ve yayın katsayıları eşit olduğundan siyah cisim; aynı zamanda, yüzey yüklerinde uyarım şekline dönüşen ısı enerjisinin tümünü enerji ışıması şeklinde yayan cisimdir. Diğer bir deyişle siyah cisim, üzerine düşen enerjisi soğurduğu gibi sahip olduğu enerjiyi de yayabilen bir cisimdir. Eşitlik 1 de e = 1 konursa, tüm siyah cisimlerin ışıma gücünün, herhangi 1 cm2 için, aynı sıcaklıkta birbirine eşit olduğu görülür. Bunun sonucu olarak; ısı ışımalarının tüm özellikleri bütün siyah cisimler için aynıdır. denilebilir. Şekilden görüldüğü gibi belli bir dalga boyu için, \rm I( \lambda T) sıcaklık yükseldikçe artar. \rm I( \lambda T) 'nin bu bölgedeki tüm dalga boyları üzerinden integrali eğri ile \rm \lambda ekseni arasında kalan alanı verir. Bu alan (1) bağıntısı ile tanımlanan I(T) büyüklüğüne eşittir vr sıcaklığın dördüncü kuvveti ile değişim gösterir. Her sıcaklığa ait tepe noktası T yükseldikçe küçük dalga boylarına yaklaşır. Bu sonuç günlük yaşantımızdaki gözlemlerimiz ile uyum halindedir. Cismin sıcaklığı arttıkça yaydığı ısı çoğalır. Uzun süre ısıtılan cisimlerin önce görünen radyasyon içinde donuk kırmızı, sıcaklık arttıkça maviye kadar değişim gösteren ışınım yaydığı bilinir. Verilen bir sıcaklık için deneysel olarak elde edilen enerjinin dalga boyuna göre değişim eğrileri, cismin cinsine bağlı olmaksızın aynı özelliği taşır. Eğrilerin tepe noktalarına ait dalga boyları \rm \lambda_{max} ile T arasında \rm \lambda_{max}T = Sabit (3) şeklinde bir bağıntı vardır. Buna Wien Yer Değiştirme Kanunu denir. Wien, siyah cismin yaptığı radyasyon ile ilgili enerji yoğunluğu \rm I( \lambda ) için, son şeklinde gözlenecek eğriyi belirleyecek biçimde aşağıdaki bağıntıyı önermiştir. \rm I( \lambda ) = c_1 \lambda^{-5} e^{-c_2/ \ \lambda T} (4) Bu bağıntı özellikle kısa dalga boyları için duyarlı değerler verir. Siyah cismin dalga boylarına göre verdiği enerji dağılımı hakkında diğer bir bağıntı Rayleigh-Jeans tarafından önerilmiştir. \rm I( \lambda ) = { 8 \pi K \over \lambda^4 } T = cT \lambda^{-4} (5) Bu bağıntı daha ziyada uzun dalga boylarında geçerli olabilmektedir. Bu eşitliğe göre \rm \lambda sıfıra yaklaştıkça \rm I( \lambda ) sonsuza yaklaşmaktadır. Bu boşluktaki enerji yoğunluğunun sonsuz olduğunu gösterir ki bu imkansızdır. Rayleigh-Jeans formülünün neden geçersiz olduğunu açıklayabilmek için, her dalga hareketi için, her dalga hareketinin enerjisinin belirli bir birim enerji, \rm \varepsilon ' un tam katları olduğunu düşünelim. Bu durumda enerji dağılımı Enerji 0 \rm \varepsilon \rm 2 \varepsilon \rm 3 \varepsilon . . . Sayı no n1 n2 n3 . . . şeklinde gösterilebilir. Dağılımın Boltzmann Dağılımı ile gösterildiğini kabul edersek \rm n_i = n_o e^{- \varepsilon / kT} (6) olduğunu yazabiliriz. Bu varsayımları kullanarak toplam tanecik sayısı N ve toplam enerjiyi hesaplayabiliriz. \rm N = \sum_{n=1} n_o + n_o e^{- \varepsilon / kT} + n_o e^{- 2 \varepsilon / kT} + n_o e^{- 3 \varepsilon / kT} + ... (7) ve \chi = e^{- \varepsilon /KT } olduğu tanımlanırsa, yukarıdaki eşitlik \rm N = n_o ( 1+ \chi + \chi^2 + \chi^3 + ... ) (8) şeklini alır. Parantez içindeki toplam 1/( 1 - \chi ) in seriye açılmış şeklidir. Bu nedenle toplam tanecik sayısı \rm N = {n_o \over 1 - \chi } (9) olarak gösterilebilir. Ortalama enerji \rm \overline{E} 'nin hesaplanması için toplam enerji aşağıdaki şekilde yazılabilir. \rm N\overline{E} = n_o.0 + n_1(\varepsilon) + n_2( 2 \varepsilon) + n_3( 3 \varepsilon) + ... \rm N\overline{E} = \varepsilon (n_1 + 2n_2 + 3n_3 + ...) \rm N\overline{E} = n_o \varepsilon ( \chi + 2 \chi^2 + 3 \chi^3 + ...) \rm N\overline{E} = n_o \varepsilon \chi( 1 + 2 \chi + 3 \chi^2 + ...) (10) ayrıca; \rm 1 + 2 \chi + 3 \chi^2 + ... = { d ( 1 + \chi + 2 \chi^2 + 3 \chi^3 + ... ) \over d \chi} = { 1 / (1 - \chi) \over d \chi} = { 1 \over (1 - \chi)^2 } (11) bu matematiksel bağıntının kullanımı ile \rm N \overline{E} = { n_o \varepsilon \chi \over (1 - \chi)^2 } (12) şeklini alır. N ve \chi 'in karşılıkları yerine konursa ortalama enerji \rm \overline{E} = { \varepsilon e^{- \varepsilon/kT} \over 1 -e^{- \varepsilon /kT } } = { \varepsilon \over e^{ \varepsilon /kT} - 1 } (13) olarak bulunur. Ortalama enerji ile dalga boyları \lambda ile \lambda \pm d \lambda arasında olan hareketlerin bileşen sayısının çarpımı, dağılım fonksiyonunu verir. \rm I( \lambda ) = { 8 \pi \over \lambda^4} \Big( { \varepsilon \over e^{ \varepsilon /kT} - 1 } \Big) (14) Planck \varepsilon ' un dalga boyu ile ters orantılı olduğunu kabul etmiştir. Frekans \upsilon = c / \lambda olduğundan \varepsilon frekans ile doğru orantılıdır ve \rm \varepsilon = h \upsilon = hc / \lambda (15) eşitliği ile gösterilir. \rm I( \lambda ) = { 8 \pi hc \over \lambda^5} \Big( { \varepsilon \over e^{ hc/kT \lambda } - 1 } \Big) (16) olduğu bulunur. Dağılım fonksiyonu \rm I( \lambda ) 'yı maksimum yapan dalga boyu \rm \lambda_{max} ise; bu eşitliğin \rm \lambda 'ya göre türevinin sıfıra eşitlenmesi ile bulunur. Bu şekilde; \rm \lambda_{max}T = { hc \over 4.965k} (17) olduğu yazılabilir. \rm \varepsilon değeri değişik grupların enerjileri arasındaki farktır. Klasik prensiplere göre; sürekli bir enerji dağılımının olabilmesi için bu enerji farkının sıfır olması gerekir. Halbuki Planck'ın \rm \varepsilon = h \upsilon varsayımı, enerji farkını sonlu yapmıştır. Ancak sonsuz uzunluktaki dalga boyları için fark sıfır olmaktadır. Siyah cisimde boşluğa yayılan radyasyon \rm h \upsilon 'nün tam katları kadar enerji verebilir. Bu nedenle yayılan enerji sürekli bir dağılıma sahiptir. Enerji kuant adı verilen parçacıklar halinde yayılır. Siyah Cisim Işıması İle İlgili Etkileşimli Sorular Bir yıldızın yüzey sıcaklığını hesaplamak Bir cismin sıcaklığı ile maksimum ışıma yaptığı dalgaboyu Siyah cisim ışıması ve belli dalga boyunda sıcaklığın fonksiyonu olarak radyasyon şiddetinin değişimi Planck Kuantum Kurami Siyah cisim ışımasında gözlenen bu olayı açıklayabilmek için 1900 yılında M. Planck kuantum kuramını önermiştir. Planck, ışıma enerjisinin ancak belli büyüklüklerde soğrulup yayımlanabileceğini yani kuantumlar halinde alınıp verileceği ileri sürülmüştür. Her kuantum enerjisi, ışımanın frekansı \upsilon ile orantılıdır. \rm \varepsilon = h \upsilon = hc / \lambda (1) Burada h Planck sabiti olup değeri 6.626x10-34 J.s dir. Işımanın frekansı arttıkça kuantumun enerjisi ve kuantumlardan oluşmuş enerji akımı olarak tanımlayabileceğimiz ışımanın enerjisi de artar. Bu nedenle siyah cisin ışımasında sıcaklık yükseldikçe yayımlanan ışıma gittikçe daha kısa dalga boylarına doğru kayar.